В рубрику "Решения корпоративного класса" | К списку рубрик | К списку авторов | К списку публикаций
При организации системы физической защиты особо важного объекта используется классический принцип [1] оптимального расположения зон безопасности и размещения в них эффективных технических средств защиты (обнаружения и противодействия) [2]. Активные средства наблюдения, с точки зрения автора, являются перспективным компонентом для применения в составе систем физической защиты (СФЗ), и их характеристики позволяют определить факт появления нарушителя и основные параметры его движения в контролируемой зоне объекта, решающего задачу противодействия нарушителю, которую можно рассматривать в рамках вероятностного подхода [3].
В рамках исследовательской задачи наиболее полным математическим описанием передвижения правонарушителя в контролируемой зоне является многомерный случайный вектор H. Отдельные характеристики (вооруженность, подготовленность и т.д.) нарушителя в этом случае описываются дифференциальными распределениями значений характеристик и их корреляционной матрицей.
Так как основой для модели является случайная величина в каждой точке контролируемой зоны и описывается она вероятностью перехода объекта из одного состояния в другое, то стоит использовать представления теории вероятностей и функционального анализа. Как известно, случайная величина полностью задается в том случае, если определить ее функцию распределения [3]. Задание функции распределения эквивалентно заданию функции плотности распределения. Для движущегося нарушителя в контролируемой зоне время пребывания в каждой точке пространства не равно нулю, и поэтому нам важно выяснить, где функция распределения (которая непрерывна в точке наблюдения активными средствами) не равняется нулю.
Для движущегося нарушителя в контролируемой зоне объекта время пребывания в каждой точке пространства не равно нулю и поэтому для нас важно, где функция распределения, которая непрерывна в точке наблюдения активными средствами, не равняется нулю. Начало отсчета движения нарушителя начинается с момента его обнаружения (в рассматриваемой точке появления нарушителя в зоне обнаружения средства наблюдения – РЛС мм диапазона, разбитой на клетки поля мгновенных плотностей вероятностей, которое и будет характеризовать систему средств наблюдения по свойству обнаружения нарушителя контролируемой зоны) [4]. Для клетки поля контролируемой зоны найдем область, в которой вероятность обнаружения нарушителя будет вычисляться на основе алгоритмов, заложенных в вычислителе активного средства наблюдения. Проведем сравнение заданной вероятности обнаружения нарушителя с расчетной на всем пути движения нарушителя до объекта защиты с учетом принимаемых допущений для решаемой задачи.
Допущение № 1. Нарушитель обнаружил воздействие технических систем наблюдения ТСО на себя, и траектория его движения к объекту защиты меняется, теперь он будет двигаться так, чтобы потратить минимальное время на достижение объекта защиты.
Пусть вероятность W данного события зависит от нескольких случайных величин S1, S2, S3, ..., Sn, также известна условная вероятность события А при заданных значениях этих величин ω (S1, S2, S3, ..., Sn). Пусть известен закон распределения совокупности этих величин, заданный плотностью вероятности ϕ (S1, S2, S3, ..., Sn). Вероятность W определяется по интегральной формуле полной вероятности [5]:
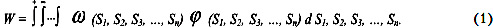
Допущение № 2. Сказанное выше в полной мере относится как к одному нарушителю, так и к группе, причем это относится к работе всего комплекса, а также к специализированным системам, являющимся составными частями ИК СФЗ.
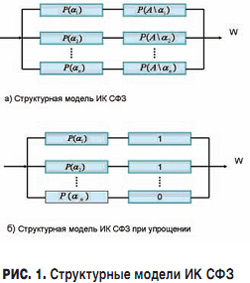
Допущение № 3. При расчетах эффективности N сложных систем, входящих в состав ИК СФЗ особо важных объектов, построим [4] структурную модель (рис. 1), на которой изобразим возможные состояния комплекса Si, характеризуемые значениями параметра αi. Данные состояния условно изображаются в виде элемента с соответствующими значениями вероятностей их появления P(αi).
Это производится по следующим правилам [5]: при последовательном соединении элементов модели (систем комплекса) их значения вероятностей перемножаются; при параллельном – складываются.
Вместе с каждым элементом модели Si последовательно изображается элемент, в котором указывается значение вероятности Р(А/αi) (рис. 1а). Структурная модель при упрощении ИК СФЗ для одномерной структуры представлена на рис. 1б. Если при всех значениях параметра α1, α2, ..., αn условные вероятности Р(А/α1), Р(А/α2), ..., Р(А/αn) принимают значения, равные 1 или 0, то структура комплекса становится одномерной.
Для одномерной системы условные вероятности можно определить следующим образом [4]:
Р(А/αi) = 1, при αi>α*iи
Р(А/αi) = 0, при αi≤α*i
или (2)
Р(А/αi) = 1, при αi<α*iи
Р(А/αi) = 0, при αi≥α*i.
К числу одномерных моделей можно отнести все устройства комплекса только в том случае, если значения их параметров αi превышают некоторое значение α*i.
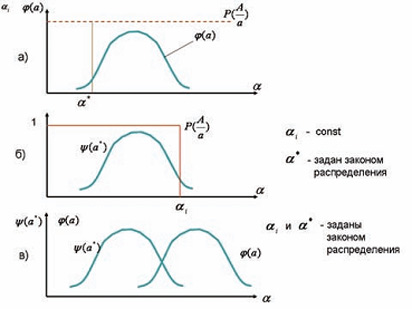
Эффективность одномерной системы, состоящей из двух активных средств наблюдения, определим следующим образом [5]. Структурная модель простой системы, к которой можно отнести систему из двух активных средств наблюдения, представлена на рис. 1б. Параметр системы задан законом распределения ϕ(α) и α* = const (рис. 2а), тогда значение вероятности определяется таким образом:
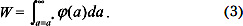
Значение функции Р(А/αi) = f(αi) устанавливается экспериментально. Если параметр системы равен постоянной величине (const), а значения α* заданы законом распределения ψ(α*) (рис. 2б), то вероятность W определяется выражением:
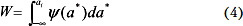
Если α и α* заданы законом распределения (рис. 2в), тогда вероятность определяется выражением:
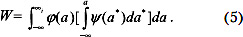
Если ф(а) и ψ(а) представлены нормальным законом распределения, выражение (5) можно преобразовать к виду:
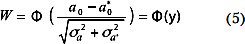
где Ф(y) – табулированная функция Лапласа [6]:
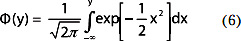
а0 и а *0 - средние значения функций ф(а) и ψ(а );
аа и аа* - среднеквадратические отклонения функций ф(а) и ψ(а*).
Из приведенных рассуждений следует, что для простых (одномерных) систем понятия эффективности и надежности
в данном случае эквивалентны, так как при всех возможных значениях параметра α1, α2, ..., αn условные вероятности Р(А/α1), Р(А/α2), ..., Р(А/αn) принимают значения, равные 1 или 0.
Проведем анализ для определения влияния тактико-технических параметров ИК СФЗ на эффективность решения задачи (под эффективностью понимается вероятность наиболее полного выполнения задачи по предотвращению возможных действий нарушителя).
Допущение № 4. При формализации модели для оценки эффективности ИК СФЗ использовались тактико-технические характеристики комплекса: факт обнаружения нарушителя; угол направления движения внешнего нарушителя относительно линии визирования активного средства наблюдения; расстояние до нарушителя; время движения нарушителя относительно объектов защиты в контролируемой зоне.
Вариант 1. Вероятности выполнения отдельных этапов работы комплекса максимальны, между собой они равны, то есть Р1 = Р2 = Р3 = Р4 = 0,95; вероятность надежной работы ИК СФЗ Рн = 0,95; вероятность выполнения задачи комплекса при противодействии внешнего нарушителя примем Рпр = 1.
Вариант 2. Вероятность подготовки ИК СФЗ к применению примем Р1 = 0,95; выполнение отдельных этапов работы комплекса будем считать минимальным и примем равными, то есть Р2 = Р3 = Р4 = 0,67; вероятность
надежной работы ИК СФЗ Рн = 0,95; вероятность выполнения задачи комплекса при противодействии внешнего нарушителя примем Рпр = 1.
Вариант 3. Вероятность подготовки ИК СФЗ к применению примем Р1 = 0,95; выполнение отдельных этапов работы комплекса будем считать минимальным и примем равным, то есть Р2 = Р3 = Р4 = 0,67;
вероятность надежной работы ИК СФЗ Рн = 0,95; вероятность выполнения задачи комплекса при противодействия внешнего нарушителя примем Рпр = 1.
Результаты расчетов для поэтапной оценки эффективности ИК СФЗ и вычисления полной эффективности W’ сведены в таблицу.
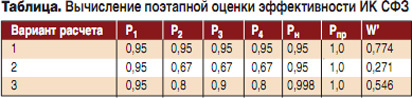
Полученные результаты позволяют оценить эффективность работы ИК СФЗ. Однако на основании принятых допущений принимаем, что поэтапная оценка применений комплекса и полученные результаты являются приближенными. На практике применение ИК СФЗ представляет собой единый процесс, этапы которого связаны между собой более сложными аналитическими зависимостями. Для более точных вычислений можно использовать программный комплекс [7], позволяющий проводить более точные расчеты с использованием тактико-технических характеристик комплекса.
Используя такие подходы в применении статистических методов теории операций и теории игр [2], можно определить влияние параметров ИК СФЗ и для других этапов применения комплекса, влияние параметров на полную эффективность выполнения задачи в целом.
Литература
Опубликовано: Журнал "Технологии и средства связи" #4, 2010
Посещений: 6553
Статьи по теме
Автор
| |||
В рубрику "Решения корпоративного класса" | К списку рубрик | К списку авторов | К списку публикаций
