В рубрику "Решения корпоративного класса" | К списку рубрик | К списку авторов | К списку публикаций
Вадим Гойхман
Алиса
Лапий
Сегодня нейронные сети успешно и широко применяются в различных сферах деятельности: медицине, экономике, связи, робототехнике и др. [1]. Одной из задач, решаемой с помощью нейронной сети, является задача классификации. Характерный пример решения этой задачи – распознавание образов, нашедшее применение в распознавании рукописного текста [2], дорожных знаков [3] и т.д. В настоящее время на нейронных сетях созданы системы, которые могут распознавать речь [4].
Динамика развития инфокоммуникационных сетей приводит к радикальному изменению структуры трафика. В настоящее время существует множество подходов к анализу трафика, но нет однозначного представления о том, какими распределениями вероятностей он описывается. Реальный трафик сети доступен в виде статистических данных о нем. Для исследования инфокоммуникационных сетей нужны адекватные методы моделирования реального трафика, для этого необходимо по статистическим данным выявить характеристики реального трафика. Одним из инструментов решения данного вопроса являются нейронные сети. Так как нейронные сети интенсивно используются в задачах классификации, представляется возможным разработать архитектуру нейронной сети для определения вероятностных распределений.
Наиболее изучены подходы при оценке телефонного трафика в системах с коммутацией каналов [5]. Описание моделей потоков в классических телефонных сетях преимущественно производилось при помощи распределения Пуассона [6]. Подходы к решению задач оценки нагрузки на сеть основаны на теории Эрланга, которая применима и к пакетным сетям [7]. Наиболее распространенными распределениями, описывающими поведения трафика NGN-сетей, являются распределения Парето, Вейбулла и логнормальное [8, 9, 10]. Трафик на малых интервалах функционирования может быть описан при помощи гиперэкспоненциального распределения [11].
В связи с этим для исследования было выбрано 6 вероятностных распределений – распределение Пуассона, нормальное распределение, лог-нормальное распределение, распределение Вейбулла, распределение Парето и гиперэкспоненциальное распределение. Целью работы является создание нейронной сети для выявления вероятностных распределений.
Для реализации нейронных сетей существуют различные программные средства: Matlab, Python, RStudio, C++ и др.
В связи с удобным графическим интерфейсом и необходимыми встроенными функциями в качестве инструмента для работы с нейронными сетями была выбрана программа Matlab. С инструментария данной программы можно создавать, обучать, использовать сеть, а также варьировать ее параметры.
В целях ознакомления с возможностями нейронных сетей в области классификации построим нейронную сеть, позволяющую распознавать одну из следующих функций: y1 – распределение Пуассона, y2 = x.^2, y3 = x, y4 = sin(x), y5 = cos(x), y6 – вектор нулей.
Одной из основных проблем при создании нейронной сети является выбор ее архитектуры, а именно подбор параметров, таких как количество слоев, количество нейронов в слое, количество обучающих выборок. Для решения поставленной задачи будем постепенно увеличивать значения данных параметров и опытным путем подбирать подходящую структуру сети.
Создана сеть, на вход которой подается вектор значений функций, состоящий из 100 отсчетов. В качестве целевого вектора обучения выбрана матрица 6х6 с единицами в главной диагонали. Каждый вектор столбец данной матрицы "кодирует" одно из известных распределений. В качестве функции активации выходного слоя выбрана функция Softmax. Данная функция позволяет вычислить выходные значения по входным, при этом значения на выходе лежат в диапазоне от 0 до 1 и представляют собой величины вероятности принадлежности входного сигнала одному из классов. Соответственно, на выходе сеть возвращает вектор-столбец, состоящий из 6 строк, каждая строка которого показывает, с какой вероятностью поданная на вход функция соответствует каждой из известных.
В качестве критерия успешности распознавания принято, что если значение в одной строке превышает 0,8, то считается, что сеть отнесла входные значения к данному распределению.
Необходимо подобрать архитектуру сети (количество слоев, количество нейронов в слое и количество выборок обучения) так, чтобы сеть правильно распознавала распределение, подаваемое на вход. Для каждой функции на каждом этапе было проведено 100 экспериментов. Под одним экспериментом подразумевается подача на вход нейронной сети одной из известных функций с зашумленными значениями.
На первом этапе происходил выбор подходящего количества нейронов в одном скрытом слое путем увеличения от 10 до 130 с шагом 20. Обучение нейронной сети происходило на матрице неискаженных значений выбранных функций. На рис. 1 показан график зависимости вероятности ошибки (в %) распознавания вектора на входе нейронной сетью при увеличении числа нейронов в скрытом слое. По данным, полученным в ходе эксперимента, можно отметить, что при 30 нейронах в одном промежуточном слое наблюдается падение вероятности ошибочного распознавания, и данная вероятность принимает минимальное значение для большинства зависимостей. Дальнейшее увеличение числа нейронов приносит уменьшение вероятности ошибочного распознавания только для распределения Пуассона и последовательности, состоящей из нулей, когда для остальных функций вероятность ошибки увеличивается.
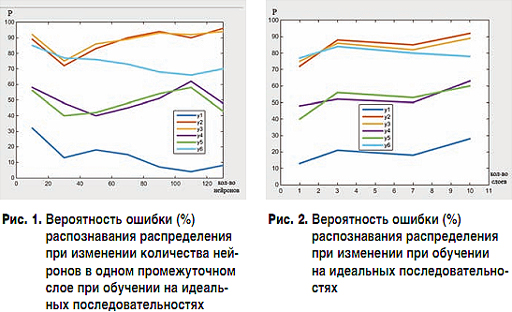
На втором этапе происходил выбор подходящего количества промежуточных слоев путем увеличения от 1 до 10. Число нейронов в слое, опираясь на предыдущий этап, выбрано 30. Обучение нейронной сети происходило на матрице неискаженных значений выбранных функций. На рис. 2 показан график зависимости вероятности ошибки (в %) распознавания вектора на входе нейронной сетью, при увеличении числа промежуточных слоев сети. По данным, полученным в ходе эксперимента, можно отметить, что увеличение числа промежуточных слоев нейронной сети ведет к увеличению вероятности ошибочной классификации вектора на входе нейронной сетью. Более того, увеличение промежуточных слоев значительно увеличивает время обучения нейронной сети.
На третьем этапе рассматривается зависимость качества распознавания нейронной сети при ее обучении на матрице с зашумленными значениями целевых зависимостей при изменении числа нейронов в одном скрытом слое, путем увеличения от 10 до 130 с шагом 20. Обучение производится на 5 видах каждой из зашумленных функций и закрепляется на функциях с неискаженными значениями. На рис. 3 показан график зависимости вероятности ошибки (в %) распознавания вектора на входе нейронной сетью, при увеличении числа нейронов в скрытом слое, при обучении сети на искаженных последовательностях исходных функций. По результатам эксперимента можно заметить, что по сравнению с обучением нейронной сети на неискаженных последовательностях обучение с зашумленными последовательностями нескольких видов и закреплением обучения на незашумленных последовательностях снижает вероятность ошибки неверной классификации нейронной сетью примерно на 30% для большинства зависимостей при 70 нейронах в одном скрытом слое. Дальнейшее увеличение числа нейронов в промежуточном слое преимущественно приводит к увеличению вероятности ошибки распознавания нейронной сети.
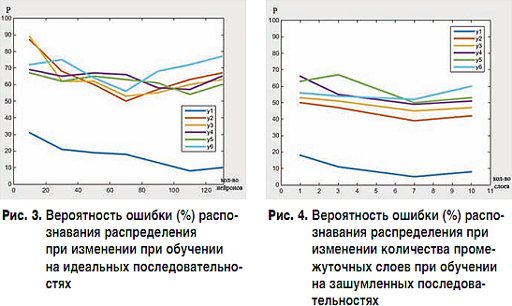
На четвертом этапе рассматривается зависимость качества распознавания нейронной сетью входного вектора при обучении сети на матрице с зашумленными значениями и увеличении скрытых слоев от 1 до 10. Основываясь на результатах предыдущего этапа, каждый промежуточный слой содержит 70 нейронов. На рис. 4 показан график зависимости вероятности ошибки (в процентах) распознавания вектора на входе нейронной сетью при увеличении числа скрытых слоев, при обучении сети на искаженных значениях исходных функций. По результатам эксперимента можно отметить, что при 7 скрытых слоях вероятность ошибки распознавания для всех классов стала меньше 60%, а для распределения Пуассона меньше – 10%. При дальнейшем увеличении промежуточных слоев наблюдается рост вероятности ошибочной классификации нейронной сетью.
На пятом этапе рассматривается зависимость качества распознавания нейронной сетью входного вектора при обучении сети на матрице с зашумленными значениями целевых зависимостей и увеличении искаженных последовательностей при обучении.
По результатам предыдущих этапов создана сеть, состоящая из 7 промежуточных слоев, каждый из которых содержит 70 нейронов. Выходной слой содержит 6 нейронов, что соответствует количеству классов, к которым мы относим значения на входе сети. Обучение нейронной сети проходит в две стадии, описанные на третьем этапе, но при этом будет увеличиваться количество обучающих последовательностей от 5 до 75 видов. На рис. 5 показан график зависимости вероятности ошибки (в %) распознавания вектора на входе нейронной сетью при увеличении числа искаженных последовательностей при обучении нейронной сети.
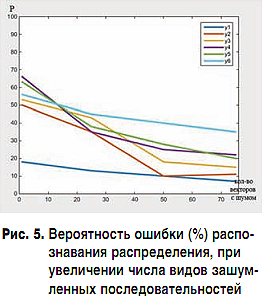
Из полученных в ходе опыта данных можно сделать вывод, что увеличение выборки для обучения нейронной сети значительно уменьшает вероятность ошибочного распознавания на входе. По характеру графиков можно сделать предположение, что дальнейшее увеличение обучающих последовательностей окажет положительный результат на классификацию нейронной сетью. Так же можно предположить, что увеличение обучающей выборки позволит уменьшить количество промежуточных слоев и нейронов в каждом слое.
Опираясь на результаты, полученные в предыдущих экспериментах, была создана сеть, которая содержит два промежуточных слоя и один выходной слой (см. рис. 6). Первый промежуточный слой имеет 30 нейронов, второй промежуточный слой – 10 нейронов, выходной слой – 6 нейронов. Обучение нейронной сети проводится на зашумленных значениях известных распределений, построенных на аргументе, сформированном случайным образом на интервале [0:3000]. Обучающая выборка содержит около 10 тыс. распределений каждого типа. В результате обучения сеть должна не просто запомнить и сопоставить значения входного вектора с выходным, а выявить взаимосвязь между обучающими последовательностями.
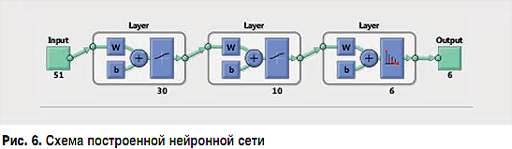
На выходе нейронная сеть возвращает вектор, состоящий из 6 значений. Каждое значение в данном векторе соответствует одному из известных распределений и показывает, с какой вероятностью распределение на входе соответствует каждому из шести классов, уже знакомых нейронной сети. Считается, что сеть корректно распознала вектор, поданный на ее вход, если вероятность на одном из выходов превышает 0,8.
Для проверки работоспособности данной сети необходимо произвести ее тестирование, которое будет осуществляться в 3 этапа по алгоритму, представленному на рис. 7.
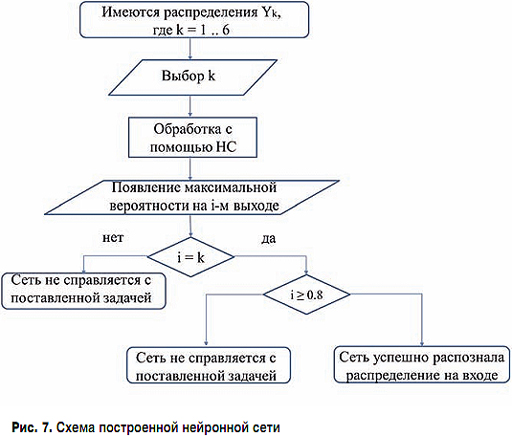
Имеется ряд распределений Yk, где k = 1, 2 ... 6 (1 – распределение Пуассона, 2 – нормальное распределение, 3 – логнормальное распределение, 4 – распределение Вейбулла, 5 – распределение Парето, 6 – гиперэкспоненциальное распределение). Из имеющихся распределений выбирается распределение k и подается на вход нейронной сети. На выходе получаем вектор, состоящий из 6 значений, и в i-й строке выходного вектора имеем наибольшую вероятность. Если i = k, то необходимо убедиться, что вероятность на i-м выходе превышает 0,8. При соблюдении данного условия считается, что сеть корректно распознала распределение, поданное на вход. Если вероятность на i-м выходе менее 0,8 или значения i и k вовсе не совпадают, необходимо произвести корректировку элементов нейронной сети или увеличить выборку при обучении нейронной сети.
На первом этапе на обученную нейронную сеть поочередно подаются вектора каждого из распределений, построенных на аргументе, изменяющемся с определенным шагом, и неискаженные шумом. В ходе эксперимента было выявлено, что нейронная сеть успешно распознает распределение Пуассона, нормальное распределение, распределение Парето и гиперэкспоненциальное распределение. На выходах, соответствующих каждому из классов исследуемых распределений, наблюдалась вероятность более 0,97. Однако сеть не справилась с классификацией логнормального распределения и распределения Вейбулла. Вероятность на третьем выходе при тестировании логнормального распределения была максимальной, но составляла 0,65, что не соответствует поставленным критериям успешного распознавания. Вероятность на четвертом выходе при тестировании распределения Вейбулла не была максимальной, что означает, что построенная нейронная сеть не смогла корректно классифицировать распределение Вейбулла при заданных параметрах.
На втором этапе на обученную нейронную сеть поочередно подаются значения каждого из распределений, построенных на аргументе, сформированном случайным образом, чтобы проверить, что сеть не просто запомнила значения, подаваемые на ее вход при обучении, но и смогла выявить зависимости между ними. В результате выявлено, что нейронная сеть успешно классифицирует нормальное распределение, распределение Парето и гиперэкспоненциальное распределение, на выходах, соответствующих каждому из классов исследуемых распределений, наблюдалась вероятность более 0,86. Для распределения Вейбулла и логнормального распределения наблюдался результат, повторяющий итоги тестирования нейронной сети на первом этапе. В связи с ограниченными программными возможностями не удалось провести анализ распознавания сетью с распределения Пуассона.
На третьем этапе на нейронную сеть поочередно подаются значения каждого из распределений, построенных на аргументе, сформированном случайным образом, а также значения самого распределения зашумлены. Тестирование показало, что нейронная сеть успешно распознает нормальное распределение, распределение Парето и гиперэкспоненциальное распределение, на выходах, соответствующих каждому из классов исследуемых распределений, наблюдалась вероятность более 0,8. Для распределения Вейбулла и логнормального распределения наблюдался результат, повторяющий итоги тестирования нейронной сети на первом этапе.
Одним из важных аспектов при распознавании является количество значений, которое необходимо подать на вход нейронной сети для получения корректного результата. Уменьшение выборки, подаваемой на нейронную сеть, позволит уменьшить ресурс, необходимый для эффективного распознавания вероятностных распределений, что может привести к сокращению времени работы сети.
Обучение и тестирование нейронной сети производилось на аргументе из диапазона [0:3000]. Постепенное уменьшение данного диапазона позволит понять, на сколько можно уменьшить количество данных, подаваемых на вход нейронной сети, при условии, что сеть будет корректно их классифицировать.
В таблице приведены значения вероятности на выходе, которые соответствуют распределению, поданному на вход нейронной сети, если значения данного распределения подавались на вход неискаженными и были сформированы на случайном аргументе.
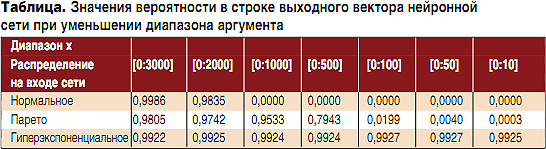
В процессе исследования было выявлено, что для распознавания нормального распределения построенной нейронной сетью необходимы значения аргумента не менее 2000, в противном случае сеть перестает успешно классифицировать нормальное распределение. Для корректного распознавания распределения Парето необходимо не менее 500 значений. Гиперэкспоненциальное распределение распознавалось построенной нейронной сетью при уменьшении диапазона аргумента до 10.
Опытным путем было установлено, что увеличивать число промежуточных слоев и количество нейронов в каждом из них можно до определенного порога. Дальнейшее увеличение данных параметров приводит к явлению "переобучения" нейронной сети – сеть перестает быть гибкой и принимает неверные решения в ходе сравнения и подстройки весов. Увеличение количества элементов сети приводит к увеличению количества связей между ними. Считается, что сети с большим количеством связей моделируют более сложные функции, которые подстраиваются под обучающие примеры, и сеть теряет способность к обобщению.
Увеличение числа последовательностей для обучения позволяет уменьшить ошибку распознавания нейронной сетью распределений, подаваемых на ее вход. При достижении определенного количества зашумленных последовательностей для обучения нейронная сеть должна обнаружить и запомнить зависимости между входными сигналами и требуемыми ответами. Возможно, увеличение обучающих последовательностей позволит снизить количество нейронов и скрытых слоев в сети, так как сеть будет обладать достаточным количеством обучающих примеров для обобщения их свойств при малом количестве связей. Однако стоит учитывать, что при увеличении выборки обучения значительно возрастает время обучения.
Тестирование показало, что нейронная сеть устойчиво классифицирует нормальное распределение, распределение Парето и гиперэкспоненциальное распределение на всех этапах. На выходах, соответствующих каждому из классов исследуемых распределений, наблюдалась вероятность более 0,8. Но построенная сеть не справилась с классификацией логнормального распределения и распределения Вейбулла. Возможно, это связано с тем, что данные распределения рассматривались при параметрах, когда их максимальные значения были близки к нулю и были мало различимы на фоне остальных распределений.
Выявлены границы распознавания вероятностных распределений построенной нейронной сети для трех распределений, успешно прошедших тестирование: нормального распределения, распределения Парето и гиперэкспоненциального распределения.
Одной из основных задач при работе с нейронными сетями является правильное построение архитектуры сети. В ходе исследования происходил анализ влияния параметров сети на ее способности к классификации. Тестирование нейронной сети позволяет выявить ее слабые стороны и определить дальнейший путь корректировки параметров.
Для получения корректного результата от нейронной сети необходимо определить количество значений, подаваемых на ее вход. Уменьшение выборки, подаваемой на нейронную сеть, позволит сократить время работы и обучения сети.
В дальнейшем на созданную и обученную нейронную сеть можно подавать не только зашумленные последовательности уже известных распределений, но также неизвестные последовательности, например значения трафика, и относить их с некой вероятностью к распределениям, которые имеются в "памяти" нейронной сети.
После проведения подобных исследований с различными видами эталонного трафика и статистическими данными с различных характерных источников можно будет определить характер и закон распределения реального трафика и осуществить его моделирование.
Литература
Опубликовано: Журнал "Технологии и средства связи" #3, 2016
Посещений: 8298
Статьи по теме
Автор
| |||
Автор
| |||
В рубрику "Решения корпоративного класса" | К списку рубрик | К списку авторов | К списку публикаций
