В рубрику "Решения операторского класса" | К списку рубрик | К списку авторов | К списку публикаций
Как известно, эффективность разнесенного приема достигается за счет декорреляции сигналов, уменьшения интервала корреляции, в результате чего замирания в канале связи становятся менее глубокими [1], и, как следствие, повышается помехоустойчивость приема сигналов.
При сравнении вариантов организации каналов связи с разнесенным приемом и комплексирования прерывистой связи с разнесенным приемом эффективность применения комплексирования будет меньше, чем выигрыш, достигаемый при использовании прерывистой связи в условиях одиночного приема. Причем выигрыш этот снижается с увеличением числа ветвей разнесения, поскольку, при этом, снижается глубина замираний, сигналы становятся все более детерминированными, а помехи похожими на белый гауссов шум.
Вместе с тем, обычно применяемое на практике использование прерывистой связи при ограниченном числе ветвей разнесения все же должно приводить к заметному увеличению помехоустойчивости. Применение разнесенного приема в условиях прерывистой связи одновременно увеличивает коэффициент использования радиолинии, что также способствует повышению помехоустойчивости приема.
Коэффициент использования радиолинии ηM представляющий собой отношение времени передачи данных в прерывистой связи к общему времени сеанса связи, существенно влияет на помехоустойчивость приема сигналов.
В условиях прерывистой связи с разнесенным приемом в каналах связи для расчета вероятности ошибочного приема сигналов необходимо определить коэффициенты использования радиолинии при различном числе ветвей разнесения (M) в зависимости от среднего отношения сигнал/шум (γ0).
Рассмотрим радиолинию с логнормальным законом замирания. При вычислении вероятностей ошибок приема сигналов ограничимся некогерентным приемом сигнала ОФМ-2.
Функция плотности вероятности при M-кратном разнесенном приеме с идеальным автовыбором при независимых логнормальных замираниях может быть определена, как и для релеевских замираний [2], из выражения
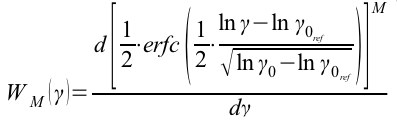(1),
где M – число ветвей разнесения, γ – текущее отношение сигнал/шум, γ0_ref. - отношение сигнал/шум в невозмущенной среде. Преобразуя (1), окончательно получим (2), (3) значения коэффициентов использования радиолинии при различном числе ветвей разнесения (M) в зависимости от γ0, при фиксированном пороге γt и γ0 ≥ γ0_ref.
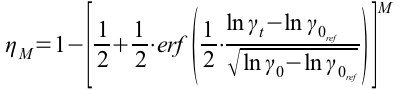(2),
а при γt=γ0
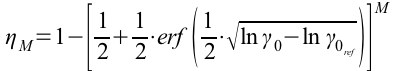(3).
В частном случае, при M = 1, отсутствие разнесения формулы (2), (3) преобразуются в (2.1), (3.1)
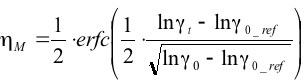(2.1),
а при γt=γ0
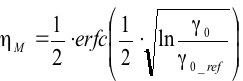(3.1)
Указанные зависимости коэффициентов использования радиолинии от γ0 (2), (3) при γ0_ref. =10 дБ, γt=γ0 и фиксированном γt=15 дБ представлены соответственно на рисунках 1 и 2.
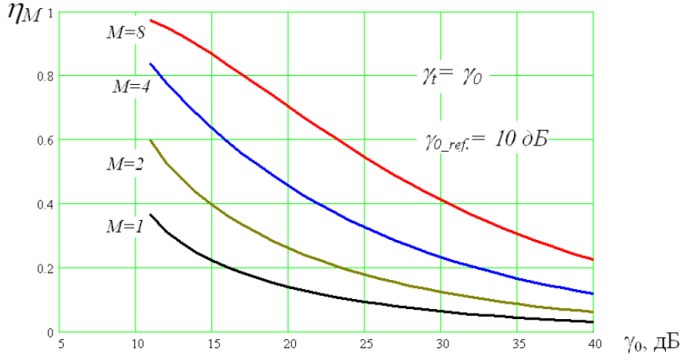
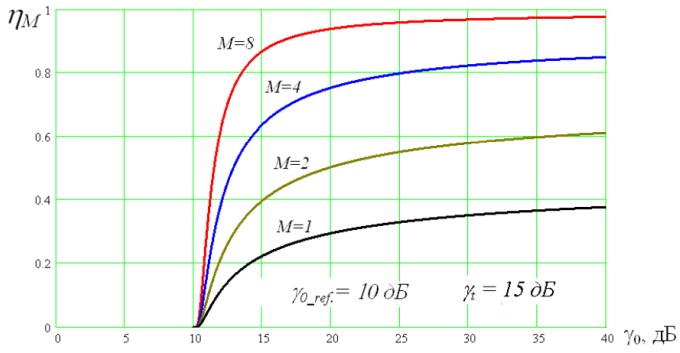
γ0 при различных М, γ0_ref. =10 дБ и фиксированном γt=15 дБ.
В отличие от релеевского канала, коэффициенты использования радиолиний в канале с логнормальными замираниями, при использовании прерывистой связи, изменяются с изменением γ0 при фиксированном γt и при γt=γ0.
При увеличении числа ветвей разнесения (M) коэффициент использования радиолиний возрастает.
При γt=γ0, с увеличением порога коэффициенты использования радиолиний снижаются, поскольку падает вероятность значений ОСШ выше порога γ0 при увеличении последнего относительно γ0_ref..
При фиксированном γt, установленном на несколько децибел выше γ0_ref. возрастание γ0, приближаясь к γt, вызывает быстрое увеличение коэффициента использования радиолиний. При значениях γ0>γt коэффициенты растут медленнее, асимптотически приближаясь к значению (1-1/2)M.
При распространении радиоволн миллиметрового диапазона, возникают флуктуации уровня огибающей (χ), распределенные по логнормальному закону. Эта мультипликативная помеха воздействует на сигнал из-за изменений диэлектрической проницаемости ε (квадрата показателя преломления волны n2), возникающей вследствие турбулентности атмосферы.
Определим возможность повышения достоверности связи этого частотного диапазона методами разнесения. Рассмотрим корреляционную функцию уровня от расстояний: вдоль распространения волны (z) и поперечной плоскости от центра диаграммы направленности (ρ) [3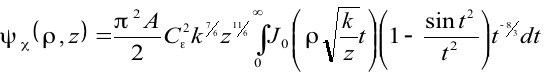,4].
(4),
где A – постоянный множитель, равный 0,033,
Cε – структурная постоянная,
k – волновое число (k = 2π/λ),
J0 - функция Бесселя первого рода нулевого порядка.
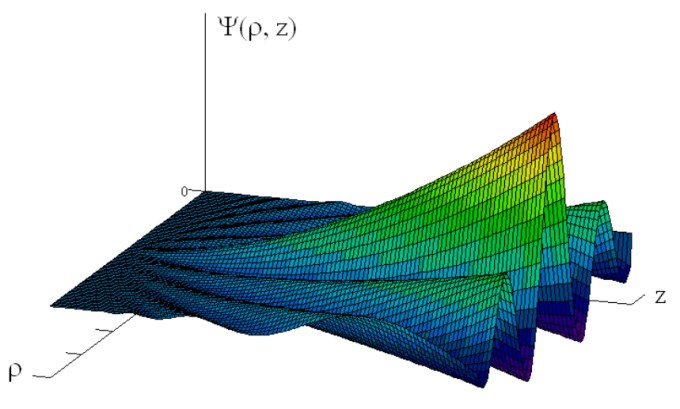
На рис. 3 представлен вид двумерной корреляционной функции, из которого видно, что уровень флуктуаций и ширина корреляционной функции вдоль ρ (перпендикулярно z) возрастают от z.
Средний квадрат флуктуаций уровня от z равен
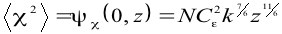(5)
где N – числовая константа, равная [3]
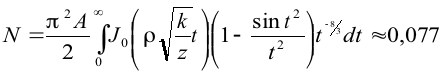(6).
Нормированная корреляционная функция, при фиксированном z, показана на рис. 4.
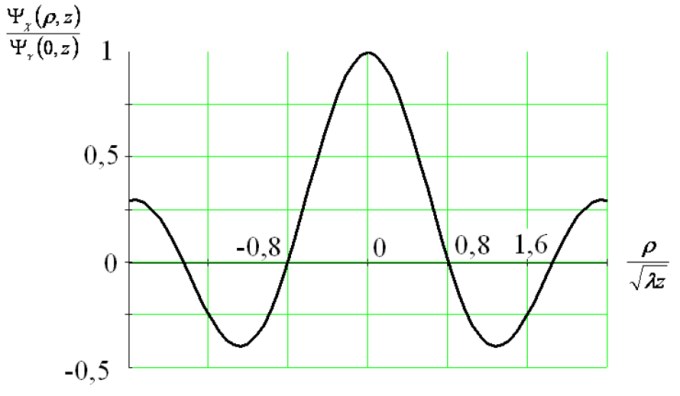
Из рис. 4 видно, что на расстоянии 30 и более километров и длине волны 7,5 мм (f=40 ГГц) ширина корреляционной функции составит 24 и более метров. В этом случае пространственное разнесение, используемое при релеевских замираниях [2], реализовать достаточно сложно, особенно для мобильных, быстро движущихся абонентов. Однако можно осуществить разнесение по углу [5]. Сигналы при этом, пройдя через разные слои турбулентной атмосферы, попадают на вход приемника практически некоррелированными. В этом частотном диапазоне узкие диаграммы направленности антенн передатчика (приемника) формируются малыми размерами апертуры антенн (технология VSAT). Для осуществления разнесенного приема по некоррелированным сигналам технологически проще изготовить антенны или ФАР небольших размеров .
Статистика логнормальных замираний определяется функцией плотности вероятности при M-кратном разнесенном приеме с идеальным автовыбором, вычислением (1), через производную интегрального распределения γ в степени числа ветвей разнесения – M.
Среднее значение вероятности ошибок некогерентного приема фазоманипулированного сигнала можно определить, аналогично случаю с релеевским каналом [2], путем усреднения вероятности ошибок в гауссовом шуме по статистике логнормальных замираний при комплексировании прерывистой связи с разнесенным приемом объединением ветвей разнесения по алгоритму автовыбора, при γt=γ0:
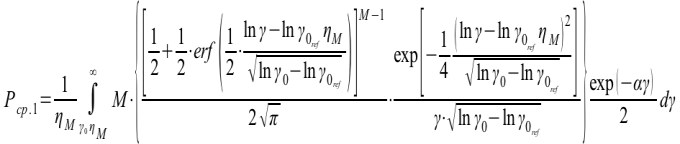, (7)
а при γt фиксированном
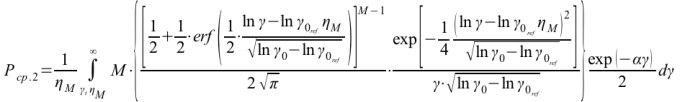, (8)
В формулах (7), (8) при M =1 подынтегральное выражение, без exp(-αγ)/2, превращается в плотность вероятности распределения γ в логнормальных замираниях при одиночном приеме [6].
Результаты зависимости указанных средних значений вероятностей ошибок (7), (8) некогерентного приема сигналов при использовании комплексирования прерывистой связи с разнесенным приемом, объединением ветвей разнесения по алгоритму автовыбора от γ0, при γ0_ref. =10 дБ, γt=γ0 и γt=15 дБ, для различных M представлены соответственно на рис. 5 и 6 в сравнении с вероятностями ошибок разнесенного некогерентного приема сигналов по алгоритму автовыбора без прерывистой связи.
Применение разнесенного приема совместно с прерыванием сигналов позволяет в каналах со случайными параметрами, в частном случае с логнормальными замираниями, во-первых, эффективно уменьшить вероятность ошибки при приеме сигналов, во-вторых, существенно, в сравнении с одиночной прерывистой связью [6] увеличить коэффициент использования радиолинии (ηM).
Указанные свойства позволяют использовать комплексирование прерывистой связи с разнесенным приемом для передачи мультимедийной информации, позволяющей одновременное использование различных форм представления данных и их обработки в едином объекте-контейнере.
M-кратный разнесенный прем, при достаточно большом M, позволяет осуществлять передачу указанных данных не только с подвижными, но и со стационарными объектами, поскольку, в этом случае, вероятность замирания в каждом из M-каналов невелика.
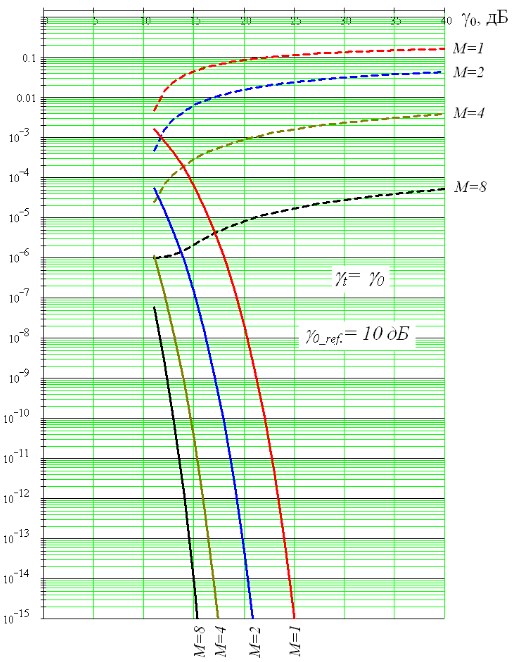
Рис.5. Зависимости: вероятностей ошибок приема сигналов при комплексировании прерывистой связи с разнесенным приемом и при объединении ветвей разнесения по алгоритму автовыбора для случая γt = γ0, γ0_ref = 10дБ с некогерентной демодуляцией (сплошные кривые) и вероятностей ошибок разнесенного некогерентного приема при объединении ветвей разнесения по такому же алгоритму без прерывистой связи для разных М в канале с логнормальными замираниями.
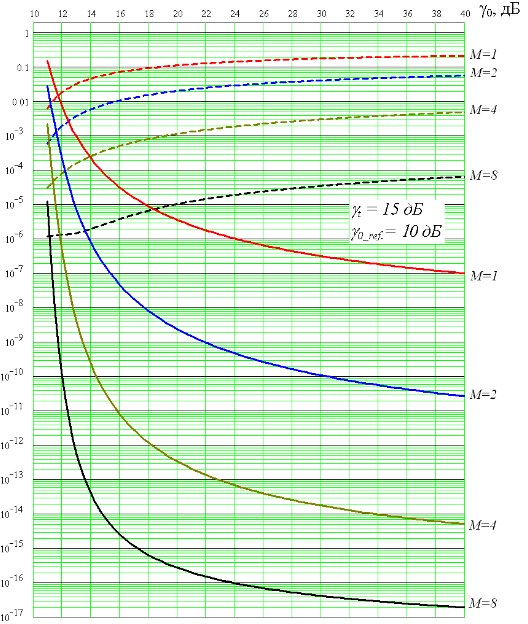
Рис.6. Зависимости: вероятностей ошибок приема сигналов при комплексировании прерывистой связи с разнесенным приемом и при объединении ветвей разнесения по алгоритму автовыбора для случая γt=15дБ, γ0_ref =10дБ с некогерентной демодуляцией (сплошные кривые) и вероятностей ошибок разнесенного некогерентного приема при объединении ветвей разнесения по такому же алгоритму без прерывистой связи для разных М в канале с логнормальными замираниями.
1. Использование разнесенного приема с объединением ветвей разнесения по алгоритму автовыбора в условиях прерывистой связи позволяет уменьшить вероятность ошибки по сравнению с одиночным приемом в условиях прерывистой связи. При этом снижается вероятность ошибки по сравнению с разнесенным приемом в каналах с логнормальными замираниями в зависимости от числа ветвей разнесения в условиях непрерывной связи при объединении ветвей разнесения по алгоритму автовыбора с некогерентной демодуляцией.
2. Представленные аналитические выражения вероятности ошибки и коэффициента использования радиолинии от среднего ОСШ (γ0) могут быть использованы для повышения эффективности организации прерывистой связи с разнесенным приемом, с объединением ветвей разнесения по алгоритму автовыбора в каналах с логнормальными замираниями.
3. Зависимость вероятности ошибки при фиксированном значении порога (γt) уменьшается быстрее при увеличении M, γ0_ref и γ0 относительно γ0_ref., что особенно актуально, учитывая ограниченность значения дисперсии в канале с логнормальными замираниями. При равенстве γ0 и γ0_ref дисперсионная составляющая сигнала отсутствует, канал детерминирован.
4. Комплексирование прерывистой связи с разнесенным приемом позволяет передавать мультимедийную информацию и осуществлять связь не только с подвижными, но и со стационарными объектами.
Опубликовано: Журнал "Технологии и средства связи" #2, 2009
Посещений: 7191
Статьи по теме
Автор
| |||
В рубрику "Решения операторского класса" | К списку рубрик | К списку авторов | К списку публикаций
