В рубрику "Спутниковая связь" | К списку рубрик | К списку авторов | К списку публикаций
The article compares the classical phase-modulated signals with a constant envelope and the radio signals used in modern satellite radio communication, formed on the basis of the Nyquist algorithm. Addresses issues of standardization of signals in satellite radio communication, laying out principles to ensure economic use of frequency resources and approach the limits of immunity. The analysis of the influence on the spectral characteristics of some characteristics of the transmission path. We investigate the parameter characterizing the signals average out-band power. Graphic shows the obtained dependence for the spectral density of the average power and out-band power considered types of radio signals.
Михаил
ГерманЗадача эффективного использования частотного ресурса является актуальной для всех приложений спутниковой радиосвязи. Она всегда требовала больших затрат на создание космического сегмента, что во многом определяет относительно высокую стоимость используемого частотного ресурса. Данное обстоятельство способствовало развитию эффективных и, как правило, сложных алгоритмов формирования и обработки радиосигналов, обеспечивающих экономное использование частотного ресурса и высокие показатели помехоустойчивости. Полученные в спутниковой отрасли технические инновации далее успешно используются в других видах радиосвязи.
Соответственно к современным системам спутниковой связи предъявляются жесткие требования, в первую очередь по экономному использованию частотного ресурса, высокой помехоустойчивости приема радиосигналов при условии минимизации дополнительной задержки в линии связи. Данные требования интегрируются с активно развивающимися современными тенденциями, связанными с повышением скорости передачи информации, развитием мобильных VSAT-систем, освоением новых высокочастотных диапазонов, пространственным и поляризационным разделением сигналов, созданием систем с многолучевыми антеннами и т.д.
Современный уровень высокоскоростных цифровых технологий позволяет использовать принципы формирования и обработки радиосигналов, близкие к оптимальным. Теоретические пределы пропускной способности Гауссова канала связи определены теоремой Шеннона [1], их достижение предполагает бесконечно большое время анализа при бесконечно большом ансамбле сигналов. Приближение к пределу Шеннона возможно за счет перехода от двоичных символов к передаче кодовых слов при соответствующем расширении полосы частот и увеличении времени на обработку сигналов, что реализуется, в частности, в результате использования сигнально-кодовых конструкций (СКК). Количественная оценка эффективности выбранных сигналов, методов их формирования и обработки часто проводится сравнением их помехоустойчивости с показателями оптимального поэлементного приема некодированных противоположных сигналов либо с пределом Шеннона, а также сопоставлением занимаемой полосы частот.
Стандартизация используемых в спутниковой связи принципов и алгоритмов формирования и обработки сигналов осуществляется заинтересованными международными организациями. Некоторые технические решения, описанные в открытых стандартах, внесшие, по мнению авторов, заметный вклад и определившие направление развития сигналообразования в спутниковой радиосвязи, приведены в табл. 1.
В настоящее время компания Intelsat ограничивает возможности ознакомления с их открытыми стандартами, поэтому удобнее ориентироваться на доступные документы ETSI (European Telecommunications Standards Institute). Как правило, нормы Intelsat и ETSI на аналогичные параметры систем связи совпадают, но иногда несколько отличаются (например, нижние границы шаблона на спектральной плотности средней мощности (СПСМ), заданные в IESS 308 и в EN 302307 для параметра α = 0,35).
В нормах на DVB-S2 (EN 302307) сформулированы современные принципы сигналообразования спутниковой связи. Данный стандарт широко используется (в ряде случаев с некоторыми ограничениями или дополнениями) в спутниковых системах с многостанционным доступом для организации каналов от центральной станции к абонентским в режиме временного мультиплексирования (TDM). Использование кодовых блоков большой длины, с одной стороны, позволяет повысить помехоустойчивость приема, приближая ее к пределу Шеннона, но с другой – увеличивает суммарную задержку в линии связи, и так заметную для спутниковых линий. Наличие задержки, связанной с длиной обрабатываемого блока, позволяет использовать данные алгоритмы главным образом в высокоскоростных каналах связи. Для низкоскоростных каналов используются более короткие коды, принятые, в частности, в EN 301790 (TPC и их разновидности).
В настоящее время продолжается развитие технологий спутниковой связи. Компания iDirect в версии ПО iDX 3.2 анонсирует использование в прямом канале радиосигналов с параметрами сглаживания α = 0,20; 0,15; 0,10 и 0,05. В обратном канале связи реализуется адаптивный режим с различными значениями MODCOD, который обеспечивает работу с низкими значениями сигнал/шум.
Несколько иначе развиваются технические решения компании Newtec: в системе Sat3Play в прямом канале допускается работа с параметрами α = 0,35; 0,25; 0,20; 0,15; 0,10 и 0,05, а в обратном канале применяется модуляция Quaternary Continuous Phase Modulation (4CPM [2]) и TPC кодирование с пятью режимами MODCOD. В [2] отмечается, что разработка таких систем требует серьезных дальнейших исследований.
Современный математический аппарат позволяет решать вопросы спектральной эффективности с использованием теории сложных импульсных процессов [3], рассматриваемых, например, в [4] как групповые импульсные случайные процессы определенного порядка. Далее исследуется более простой случай узкополосной передачи независимых равновероятных информационных символов. На практике рандомизация символов обеспечивается достаточно эффективно в результате применения специальных мер, в том числе скремблирования, перемежения, передачи в общем потоке разнородной информации от многих источников, использования кодов большой длины и т.д., в связи с чем данная модель является универсальной для многих приложений.
Классическая фазовая модуляция с радиосигналами, имеющими прямоугольную огибающую, предполагает передачу символов с дискретным изменением фазы несущей на границах символьных посылок, которые могут нести информацию об одном или нескольких битах. Как уже указывалось, наиболее распространенные разновидности - это двух-, четырех- и восьмипозиционная фазовая модуляция (BPSK, QPSK, 8PSK). Радиосигналы с постоянной огибающей позволяют передатчику при односигнальном режиме работать с максимальной мощностью без спектрального разрушения сигнала. СП СМ таких независимых равновероятных радиосигналов имеет только непрерывную составляющую и описывается известным соотношением:
причем здесь и далее принято, что N = 2, 4, 8… - целое положительное число, определяющее размер выбранного ансамбля радиосигналов (например, при 8PSK N = 8), n = log2 N, T - длительность двоичного символа, Ts = T log2 N = Tn - длительность символа (интервал следования радиоимпульсов), x = (ω - ω0)T - нормированная центрированная круговая частота, ω0 = 2πƒ0 - круговая несущая частота.
Кроме СПСМ в технических приложениях иногда представляет интерес параметр, характеризующий сосредоточенность СПСМ в полосе частот 2Δω относительно центральной частоты ω0:
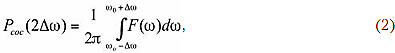
или для симметричной СПСМ
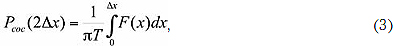
где Δx = ΔωT - нормированная к двоичному тактовому интервалу полоса анализа.
Тогда параметр, характеризующий внеполосное излучение, вычисляется из соотношения:
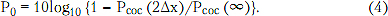
Классические радиосигналы с офсетной модуляцией могут быть представлены в виде суммы квадратурных составляющих модулированных сигналов. При этом результирующий радиосигнал имеет постоянную огибающую. Такие радиосигналы с offset QPSK, MSK, сглаженной офсетной модуляцией (СОМ) близки к сигналам с QPSK и отличаются от них тем, что за счет смещения на тактовый интервал в квадратурах у них может быть уменьшена величина фазового сдвига на границах посылок, в результате чего, соответственно, уменьшен уровень внеполосного излучения. Спектральная плотность средней мощности (СПСМ) радиосигналов с офсетной модуляцией может быть определена из известного соотношения:
где G(x) - преобразование Фурье от радиоимпульса y(τ) = cos[x0τ + φ(τ)], x0 = ω0T - нормированная круговая частота, причем для узкополосных радиосигналов справедливо:
а для получения постоянной огибающей результирующего радиосигнала с офсетной модуляцией должны выполняться условия: φ(0,5) = π/4, φ(τ) + φ(1-τ) = π/2 на нормированном тактовом интервале τ = t/T ? [0,1] .
Для offset QPSK: φ(τ) = π/4, для MSK: φ(τ) = πτ/2, для СОМ-6: φ(τ) = π/4[1 - cos (πt)] на тактовом интервале т ? [0,1]. Необходимо отметить, что в соответствии с терминологией, принятой в [5], СОМ-L означает, что L = 2(l+1), где l – целое неотрицательное число, определяемое из условия существования l-1 производных от фазы несущей φ(τ), не имеющих разрыва. Для данного условия при достаточно больших отстройках относительно несущей частоты скорость спадания СПСМ таких радиосигналов пропорциональна величине 1/x2(l+1).
Графики нормированной СПСМ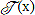 
для радиосигналов с QPSK, offset QPSK, MSK и СОМ-6 приведены на рис. 1, причем
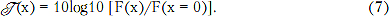
Ломаные кривые красного цвета на рис. 1 отображают шаблон (верхнюю и нижнюю границы), задаваемый нормами ETSI для СПСМ спутниковых радиосигналов с α = 0,35, пересчитанные для эквивалентного случая, соответствующего четырехфазным радиосигналам, когда Ts = 2T (то есть N = 4).
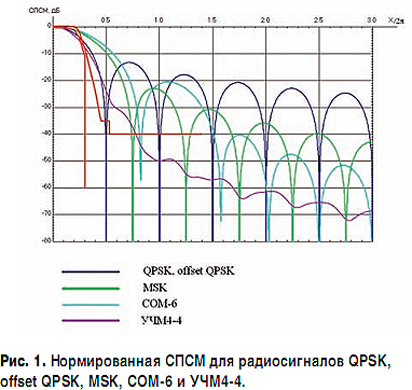
Таким образом, рассмотренные выше радиосигналы с классическими методами модуляции характеризуются постоянной огибающей радиосигнала и ограниченной длительностью радиоимпульса. Как следует из приведенных графиков, уровень внеполосного излучения сигналов достаточно большой и, следовательно, меры по ограничению изменения фазы на границах тактовых интервалов, принятые в радиосигналах с офсетной модуляцией, не обеспечивают требования по компактности СПСМ.
Радиосигналы с управляемой частотной модуляцией (УЧМ, Tamed Frequency Modulation - TFM) - это сигналы с постоянной огибающей и сглаживанием резких изменений фазы [6]. В результате такого сглаживания ансамбль сигналов увеличивается и не обеспечивается требование на противоположность сигналов, вследствие чего несколько снижается помехоустойчивость оптимального поэлементного приема (как показано в [6, 7], проигрыш составляет порядка 1 дБ в области вероятности ошибки Pош ≈ 10-8). Степень сглаживания фазовых переходов определяет коррелированность формируемых радиоимпульсов. В [5] исследовались радиосигналы УЧМ4, у которых коррелированность распространяется на 4 тактовых интервала, а количество возможных форм радиоимпульсов равна 24 = 16.
При расчете СПСМ радиосигналов с УЧМ4, не снижая общности, можно положить, что x0 = 2π (M + 1/4), где M - целое число. Тогда формы радиоимпульсов могут быть записаны следующим образом:
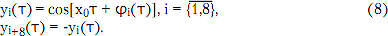
Для УЧМ4-L при L = 4 используются линейная и тригонометрическая аппроксимация, описываемая следующими функциями:
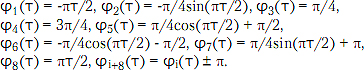
Соответственно спектральные характеристики таких радиосигналов могут быть вычислены с использованием теории сложных импульсных процессов [3], а также, например, результатов [8]:
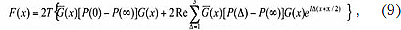
где G(x) - матрица-столбец с элементами Gi(x), для случая узкополосных радиосигналов
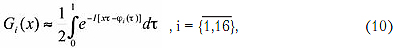
G(x) - матрица-строка с комплексно-сопряженными элементами Gi(x), P(Δ) - квадратная матрица с элементами pij(Δ) - безусловными вероятностями совместного формирования радиоимпульса формы yi(T) в любом k-м тактовом интервале и радиоимпульса формы yj(T) в любом (k-Δ)-м тактовом интервале. Учитывая, что формируемая последовательность радиоимпульсов является цепью Маркова, можно определить следующую взаимосвязь:
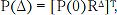
T, где R - квадратная матрица с элементами rij, характеризующими условные вероятности формирования в любом k-м тактовом интервале радиоимпульса формы yi(т) при условии, что в (k-1)-м тактовом интервале был сформирован радиоимпульс формы yj(T), i,j = {1,16}, а надстрочный знак Т означает операцию транспонирования матрицы. Для определенных выше форм радиоимпульсов и условий на несущую частоту можно записать:
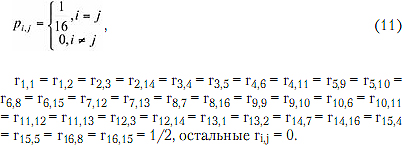
Рассчитанная в соответствии с данными соотношениями СПСМ для радиосигналов с УЧМ4-4 приведена на том же рис. 1. Другие разновидности УЧМ4, рассмотренные в [5], обеспечивают несколько худшее спадание СПСМ вблизи от несущей частоты, но большую скорость спадания СПСМ при x/2π>2.
Анализ графиков на рис. 1 показывает, что для рассмотренных типов радиосигналов с постоянной огибающей главный лепесток СПСМ близок к функции [sin(X)/X]2, а не к идеальной прямоугольной форме. Данное обстоятельство свидетельствует о недостаточности сглаживания фазовых переходов в рамках сигналов с постоянной огибающей и необходимости использования других алгоритмов формирования радиосигналов для получения компактного спектра мощности.
Для формирования сигнала, имеющего близкий к прямоугольному спектр мощности, Найквист предложил использовать сглаживающий фильтр, модуль коэффициента передачи (амплитудно-частотная характеристика, АЧХ) которого может быть записан в следующем виде:
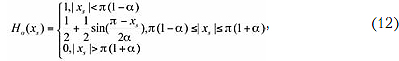
где xs = (ω - ω0) Ts - нормированная к символьному интервалу Ts центрированная круговая частота, а варьируемый параметр сглаживания 0 ≤ α ≤ 1 (коэффициент roll-off) определяет степень прямоугольности фильтра, причем чем меньше значение а, тем "прямоугольнее" АЧХ фильтра, но и тем медленнее во временной области осуществляется затухание сигнала.
Импульсная характеристика может быть определена через обратное преобразование Фурье от коэффициента передачи фильтра. В случае идеальности фильтра, при условии, что коэффициент передачи описывается вещественной функцией, она имеет вид:
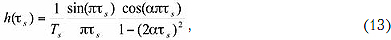
где Ts = t/Ts = т/n - нормированный к символьному интервалу параметр времени, причем символьный и двоичный тактовые интервалы связаны соотношением Ts = nT, n - целое положительное число.
Сигнал, сформированный с использованием фильтра Найквиста, характеризуется бесконечной длительностью и регулярностью (через символьный интервал) следования нулей функции, причем огибающая такого радиосигнала непостоянна. То есть в идеальном случае в тактовых точках следования символов отсутствует межсимвольная интерференция.
В то же время, как следует из теории оптимального приема радиосигналов в канале с аддитивным белым шумом, приемный фильтр должен иметь коэффициент передачи, комплексно сопряженный с формирующим фильтром. В результате прохождения такого сигнала через оптимальный приемный фильтр нарушается условие регулярности следования нулей в тактовых точках, возникает межсимвольная интерференция, вследствие чего снижается помехоустойчивость приема.
На практике алгоритм Найквиста используется в трансформированном виде, при котором сигнал принимает вид, соответствующий приведенной выше импульсной характеристике, уже после приемного фильтра, когда требуется выполнение условия отсутствия межсимвольной интерференции в тактовых точках. Следовательно, суммарная сквозная характеристика передающего и приемного трактов должна описываться коэффициентом передачи фильтра Найквиста. При этом несколько расширяются формирующий и приемный согласованный фильтры и соответственно изменяется спектр мощности излучаемых радиосигналов.
Нормы ETSI, в частности EN 302307, задают аналитическое описание модуля коэффициента передачи формирующего фильтра радиосигналов, непосредственно указывающее на реализацию алгоритма Найквиста, в следующем виде:
Нормы ETSI задают также ограничения на фазочастотную характеристику формирующего фильтра через нормированную к частоте Найквиста неравномерность группового времени запаздывания в полосе его пропускания.
Эквивалентная шумовая полоса радиофильтра равна Fш.экв =1/Ts, а частота среза (по 3 дБ) Δƒср=|ƒср - ƒо| = 1/2Ts, где ƒо - центральная частота.
Импульсная характеристика подобного идеального фильтра имеет вид:
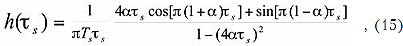
причем сформированный радиосимвол характеризуется нерегулярностью появления нулей и непостоянством огибающей. Регулярность нулей обеспечивается уже после обработки сигнала в согласованном приемном фильтре.
На практике при формировании сигнал ограничивают несколькими тактовыми интервалами в зависимости от значения параметра а, требуемой точности и возможностей реализации. СПСМ таких радиосигналов рассчитывается из следующего выражения:
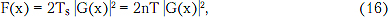
для узкополосных радиосигналов:
причем в выражении для импульсной характеристики вводится τs = τ/n и Ts = nT, а τmax = Tmax/Ts = Tmax/nT – нормированный к длине символа параметр времени, ограничивающий на практике длительность сформированного символа величиной Tmax.
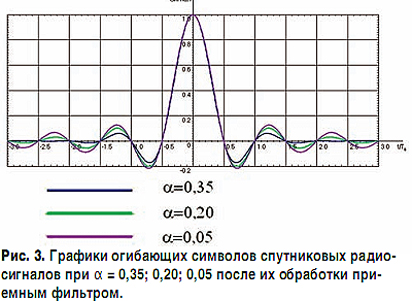
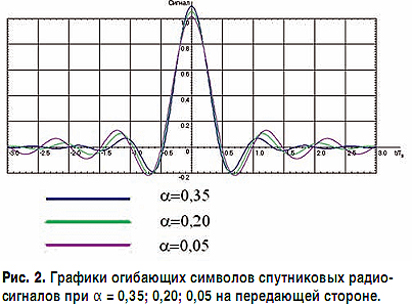
Соответственно на рис. 2 и 3 приведены графики огибающих символов спутниковых радиосигналов для значений α = 0,35; 0,20; 0,05 на передающей стороне и после их обработки согласованным приемным фильтром. Рисунки иллюстрируют эффект нормализации приемным фильтром (то есть появления регулярности) следования нулей временной функции, описывающей огибающую символа спутникового радиосигнала.
Далее приводятся результаты исследований спектральных характеристик радиосигналов спутниковых систем связи, полученные с использованием приведенных аналитических соотношений.
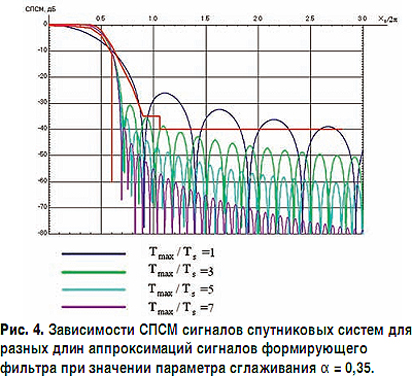
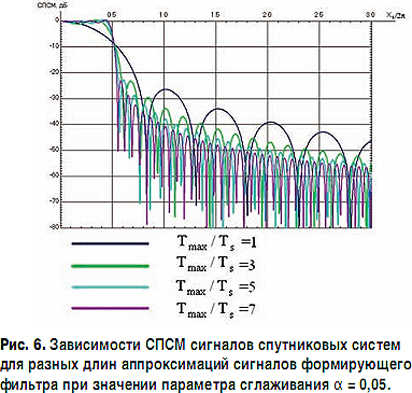
На рис. 4, 5 и 6 представлены зависимости СПСМ сигналов спутниковых систем для разных длин аппроксимаций сигналов формирующего фильтра для случаев α = 0,35, α = 0,20 и α = 0,05 соответственно, причем на рис. 4 (α = 0,35) и рис. 5 (α = 0,20) также приведены шаблоны ETSI.
Как показывают вычисления, при α = 0,35 длина аппроксимации должна быть Tmax/Ts > 3,2, при α= 0,20 - Tmax/Ts > 5,2 (нормы ETSI на СПСМ для α = 0,05 авторам не известны). Необходимо учитывать, что чем меньше значение α, тем "прямоугольнее" формирующий фильтр и тем более жесткие требования на точность посылок и их реализуемую длительность.
Сравнительные зависимости СПСМ сигналов спутниковых систем и сигналов Найквиста для случая α = 0,35 и Tmax/Ts = 7 приведены на рис. 7, из которого следует, что сигналы Найквиста имеют несколько лучшую скорость спадания боковых лепестков СПСМ, чем сигналы, используемые в спутниковых системах связи.
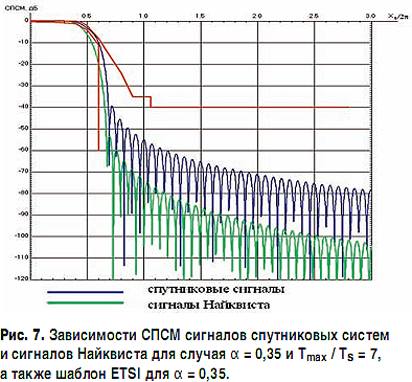
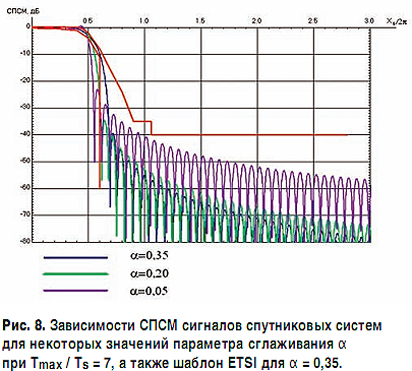
На рис. 8 приведены зависимости СПСМ сигналов спутниковых систем для трех параметров формирующего фильтра (α = 0,35; 0,20 и 0,05) при аппроксимации длительности Tmax/Ts = 7, а также шаблон для случая α = 0,35. Из рисунка видно, как с уменьшением α становится уже основной лепесток СПСМ, причем при малых значениях α возможен небольшой всплеск СПСМ вблизи среза формирующего фильтра (частоты Найквиста).
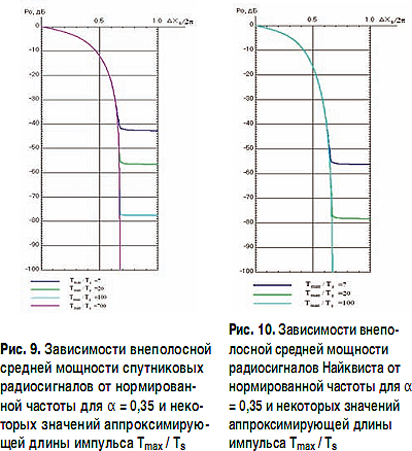
Исследование параметра внеполосной средней мощности радиосигналов целесообразно проводить с учетом идеализации принятой модели формирующего фильтра. На рис. 9 приведены зависимости внеполосной средней мощности спутниковых радиосигналов от нормированной частотной отстройки при α = 0,35 и различных значениях аппроксимирующей длины импульса Tmax/Ts, а на рис. 10 – аналогичные зависимости внеполосной средней мощности сигналов Найквиста при α = 0,35. Из графиков видно, что при увеличении Tmax/Ts внеполосная средняя мощность обоих типов сигналов стремится к асимптотической кривой, причем сосредоточенность мощности в полосе частот у радиосигналов Найквиста несколько лучше, чем тот же параметр у спутниковых сигналов.
Принимая во внимание данную особенность внеполосного излучения радиосигналов Найквиста и спутниковых сигналов, проведем сопоставление этого параметра для рассматриваемых типов сигналов. На рис. 11 представлены зависимости внеполосной средней мощности данных радиосигналов, причем для сигналов Найквиста и спутниковых сигналов, приведенных к четырехфазной системе радиосигналов, показаны асимптотические зависимости.
При расчетах, как и ранее, полагалось, что для радиосигналов, сформированных фильтром Найквиста, Pcoc(∞) = 0,5 - 0,125α, а для всех остальных типов исследуемых сигналов Pcoc(∞) = 0,5. Как следует из рисунка, наилучшую сосредоточенность средней мощности имеют сигналы Найквиста и спутниковых систем связи. Остальные радиосигналы заметно проигрывают им по данному параметру.
Полученные результаты позволяют сопоставить спектральные характеристики классических фазомодулированных радиосигналов с постоянной огибающей и сигналов, сформированных на основе алгоритма Найквиста. Сигналы, используемые в спутниковой радиосвязи, обеспечивают существенную экономию частотного ресурса. В то же время реализация современных частотно-эффективных радиосистем предполагает применение высокоскоростных цифровых технологий, сложных принципов сигналообразования, линейных передающих и приемных трактов, не приводящих к разрушению сигналов. При возникновении заметной нелинейности в таком тракте возможно резкое снижение помехоустойчивости приема и изменение СПСМ, вплоть до предельного случая, когда при жестком амплитудном ограничении в тракте спектральные характеристики приближаются к соответствующим характеристикам сигналов с классической фазовой модуляцией.
Приведенные данные могут быть использованы при анализе и проектировании новых систем связи с эффективным использованием частотного ресурса. Представленные графики позволяют оценить влияние на спектральные характеристики радиосигналов, используемых в спутниковой связи, ряда параметров формирующего тракта.
Принципы экономного использования частотного ресурса, реализуемые в спутниковой связи, очевидно, будут востребованы и для других видов радиосвязи, в частности радиорелейной.
Дальнейшее совершенствование сигналов спутниковых радиосистем будет, по-видимому, происходить путем развития теории и практики создания новых адаптивных СКК при конвергенции методов модуляции и кодирования с целью повышения эффективности использования частотного ресурса.
Кроме того, данные результаты могут быть использованы для дальнейшего развития теории сложных импульсных процессов.
Литература
Опубликовано: Журнал "Технологии и средства связи" #1, 2014
Посещений: 8278
Статьи по теме
Автор
| |||
Автор
| |||
В рубрику "Спутниковая связь" | К списку рубрик | К списку авторов | К списку публикаций
