В рубрику "Спутниковая связь" | К списку рубрик  |  К списку авторов  |  К списку публикаций

Физические ограничения при реализации многолучевых параболических антенн: минимальный угловой разнос смежных лучейPhysical limitations in the implementation of multi-beam parabolic antennas: the minimum angular separation of adjacent beams

Валентин
Анпилогов

ЗАО "ВИСАТ-ТЕЛ", к.т.н.

Александр
Афонин

Банк России, к.т.н.

В последние годы особый интерес вызывают спутниковые системы связи и вещания, космический сегмент которых реализован на основе многолучевых спутников. Такие спутники получили уже устоявшееся обозначение HTS (High Thoughput Satellite). Реализация спутников HTS и систем ШПД в целом основана на использовании многолучевых антенн, как бортовых, так и наземных (например, в системах спутникового ШПД и/или ТВ).

Учитывая, что в общедоступных публикациях системного характера, посвященных системам ШПД на основе спутников HTS, ряд ключевых вопросов реализации многолучевых антенн, как правило, не раскрывается, в статье представлены простые соотношения для оценки ограничений физической реализуемости многолучевых параболических антенн зеркального типа, которые широко применяются на практике. Вопрос о минимально достижимом угловом разносе между смежными лучами является одним из ключевых при формировании рабочей зоны на этапе проектирования современных многолучевых спутниковых систем ШПД и тем более актуален для многолучевых спутников HTS следующего поколения с пропускной способностью, характеризуемой уже в единицах Тбит/с [1], что достигается в основном за счет увеличения числа лучей до нескольких сотен (соответственно уменьшается ширина луча).

Анализу многолучевых антенн параболического типа с выносом излучателей из фокуса посвящено достаточно много работ, начиная примерно с 1970-х гг., но простых и понятных соотношений для оценки ограничений физической реализуемости многолучевых антенн в них найти непросто.

Большинство известных работ связано с оценкой допустимой точности установки облучателя в области фокуса антенны и не раскрывают существа задачи проектирования многолучевых систем. Наиболее информативные сведения для оценки ограничений углового разноса смежных лучей представлены в работе [2]. В этой работе приведены простые аналитические соотношения оценки снижения уровня усиления в луче при его отклонении от основного осевого направления. В предположении аппроксимации диаграммы направленности облучателя функцией косинуса представлены оценки уровня пересечения смежных лучей в зависимости от уровня облучения края зеркала. К сожалению, в формуле оценки уровня пересечения смежных лучей в [2] допущена опечатка (формула 20, следует под D1 подразумевать D1/λ).

Ниже более подробно представлен упрощенный метод оценки, позволяющий решить эту задачу на основе аппроксимации луча гауссовым пучком, что дает хорошее приближение до уровня - 8 дБ [3, 4] и может быть использовано вплоть до уровня, равного уровню огибающей боковых лепестков.

Постановка задачи

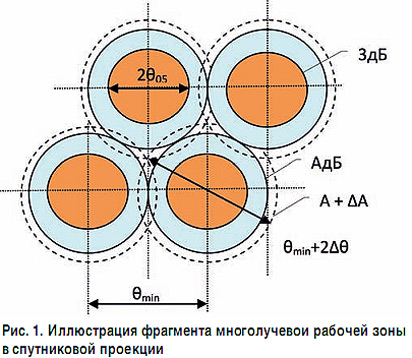
Фрагмент многолучевой рабочей зоны в спутниковой проекции показан на рис. 1, на котором представлены принятые обозначения. Требуется получить простые аналитические соотношения, определяющие взаимосвязь физических параметров зеркальной антенны и минимального углового разноса смежных лучей. Задача решается в приближении распределения Гаусса (для иных распределений существо физических зависимостей не изменится).

Геометрия многолучевой антенны иллюстрируется на рис. 2.

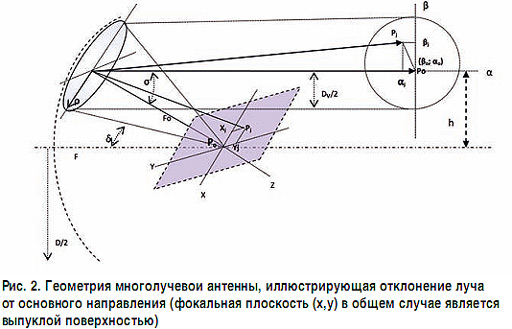
Отклоненный луч Pj характеризуется двумя угловыми составляющими αj и βj, которые отсчитываются от основного направления (α0; β0), характеризующего пространственное положение луча P0. В данном случае примем α0=β0=0. Положение излучателя, создающего луч j, определяется координатами центра его раскрыва Xj, Yj. Взаимосвязь между {Xj; Yj} и {αj; βj} задается соотношениями

где F0=F/cos²(δ/2) - фокусное расстояние для вырезки из симметричного параболоида с фокусным расстоянием F.

Геометрическое расстояние между точкой фокуса (X0; Y0) и центром излучателя (Xj; Yj) для отклоненного луча Pj дает физическое ограничение размера апертуры излучателя. Это расстояние обозначим Δd, и оно должно быть больше физического раскрыва рупорного облучателя. Таким образом, основное геометрическое соотношение, устанавливающее взаимное соответствие между величиной отклонения луча, размером апертуры излучателя и фокусным расстоянием антенны:

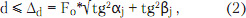
где d - диаметр апертуры рупорного излучателя (примерно равен его максимальному физическому размеру).

Дополнительно принято, что для рассматриваемых зеркальных систем лучевой коэффициент редукции близок к единице, что справедливо при значениях Fo/Dv близких и тем более больших единицы с точностью выше 3-4%.

Требуется найти простую аналитическую функциональную оценку угла Θmin, который в общем случае равен значению Pj-Po на рис. 2.

Оценка минимального углового разноса лучей

Выбор размера апертуры излучателя не может быть произвольным и зависит от требуемого угла облучения основного зеркала и его физической реализуемости. Будем считать, что излучатель создает луч с распределением поля в поперечном сечении, отвечающим пучку Гаусса [3]

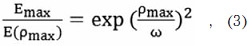
где Emax/Epmax - относительный уровень напряженности поля на краю зеркала (1-Δ);

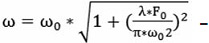
расходимость пучка;

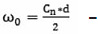
минимальный радиус пучка (Сn<1);

Рmах ? Fo * tg(δ - β) - максимальный радиус пучка на краю зеркала;

Сn - коэффициент (зависит от типа излучателя, см. табл.) [4].

Взаимосвязь параметров ω0 и d для ряда рупорных излучателей представлена в табл. [4].

Учитывая, что F0/d>>l и F0/Dv >1, соотношение (3) упрощается и приобретает аналитический вид

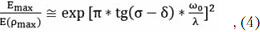
Из (4) получим аналитическую оценку размера апертуры излучателя

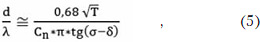
где Т = 20 Lg Emax/Epmax = - 20

Lg(l-Δ) уровень облучения края зеркала, а величина, 2 (δ - β) - угол облучения зеркала.

Учитывая ограничение (2), из которого следует d ≤ minΔd = Fo*tgθmin, и оценку (5), получим предельный минимально возможный нормированный (θmin/2θ0,5) угловой разнос смежных лучей

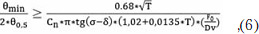
где Dv - диаметр антенны (рис. 2);

2 θ0,5 = (1,02 + 0,0135*T)*λ/Dv эмпирическая зависимость ширины диаграммы направленности антенны по - ЗдБ от уровня облучения края зеркала [6] в радианах;

Сn - типичное значение 0,64 (см. табл. 1).

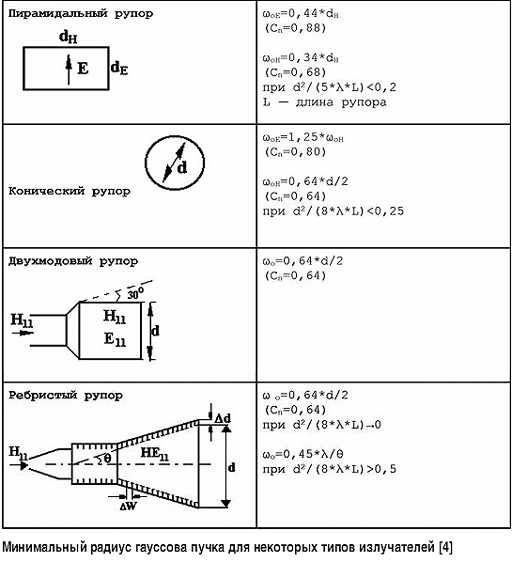
Значение (Fo/Dv) связано с tg(δ - β) довольно громоздкими соотношениями

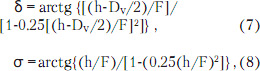
где принятые обозначения показаны на рис. 2.

Очевидно, что прямое использование (6) с учетом (7) и (8) возможно только для конкретного набора параметров зеркальной системы. Для получения обобщенной аналитической зависимости можно преобразовать tg(δ - β) с учетом (7) и (8) при условии малости (h-Dv)/F и F0/Dv >1, что дает следующее упрощенное соотношение:

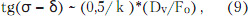
где коэффициент к близок к единице, но всегда немного менее единицы и примерно равен cos2(δ/2) в широких пределах изменения геометрических параметров несимметричной параболической антенны.

С учетом введенных приближений, принимая условие Fo/Dv>l (то есть для относительно малых δ), соотношение (6) имеет вид

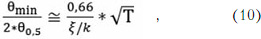
где 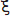= (1,02+0,0135Т) - коэффициент, определяющий изменение ширины диаграммы направленности луча в зависимости от уровня (Т, дБ) облучения края зеркала;

k - cos²(δ/2) - коэффициент, обычно близкий к единице.

Соотношение (10) дает приблизительную оценку минимально возможного нормированного углового разноса смежных лучей, формируемых в одном раскрыве многолучевой однозеркальной антенны, при использовании рупорных облучателей.

Полученные соотношения для однозеркальной антенны справедливы и для двухзеркальной антенны [2] (для этого требуется выполнить стандартное преобразование геометрии двухзеркальной антенны к эквивалентной однозеркальной).

Уровень пересечения смежных лучей и эффективность антенны

Уровень пересечения лучей (рис. 1) определяется простым известным соотношением: А ≈ 3 (θmin/2θ0,5)2, дБ А + ?А ≈ 3,5 (θmin/4θ0,5)2 , дБ , (11) Принимая во внимание (10), получим зависимость достижимого уровня пересечения смежных лучей от уровня облучения края зеркала А ≈ 1,3*T *k2, дБ , (12)

или для экспресс оценок можно принять A ~ T для широкого круга реализаций несимметричных параболических антенн.

Анализ результатов

Полученные выше результаты оценки разноса смежных лучей справедливы до уровня их пересечения 8 дБ. Как следует из представленных данных, при увеличении уровня облучения края основного зеркала многолучевой параболической антенны (уменьшение T или увеличение - T) достижимый нормированный угол θmin/2θ0,5 между смежными лучами уменьшается. Однако, как следует из теории зеркальных антенн, оптимальному значению уровня облучение края зеркала соответствует T = 10–11 дБ. При оптимальном уровне облучения (максимальный коэффициент усиления) разнос смежных лучей составит примерно 4θ0,5, а уровень А дБ их пересечения составит примерно те же T дБ. Очевидно, что можно достичь уровня пересечения смежных лучей - 3 дБ и даже более, но при этом следует облучать край зеркала на уровне выше - 4 дБ, что в конечном итоге приводит к значительному снижению коэффициента усиления луча, а боковые лепестки существенно возрастают. На рис. 3 представлен график зависимости снижения апертурного КИП (соответственно и усиления антенны) от уровня облучения края зеркала [7].

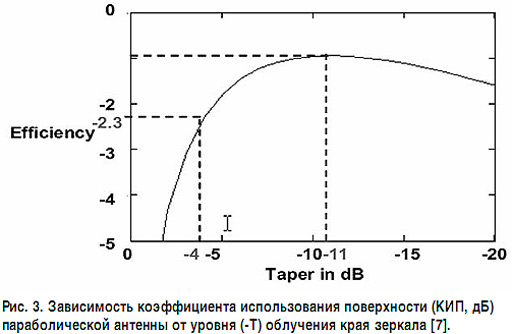
Примерная оценка коэффициента использования поверхности многолучевой антенны при T= 4–5 дБ составит 0,55, то есть коэффициент усиления в луче снизится относительно оптимального варианта облучения почти на 1,4 дБ (аналогичный результат примерно совпадает с представленным в [2]). Можно сформулировать примерное правило, которое говорит о том, что уровень пересечения смежных лучей многолучевой антенны с рупорными облучателями и относительно малым офсетным углом в нулевом приближении численно сравним с уровнем облучения края зеркала, по крайней мере не выше этого уровня.

Можно предположить, что полученные выше результаты оценки разноса смежных лучей справедливы до уровня их пересечения 8 дБ. Численная проверка показывает, что подстановка полученных значений θmin/2θ0,5 в соответствии с (10) в данной статье в формулу 20 (после исключения опечатки) в статье [2] дает отличие в уровне пересечения в пределах 10% до значений А = 8 дБ и увеличивается примерно до 15% при больших А. Таким образом, можно утверждать, что конечный результат слабо зависит от формы аппроксимации диаграммы направленности рупорного излучателя.

Выводы

Анализ реализуемого углового разноса смежных лучей в многолучевой зеркальной антенне показывает, что существуют ограничения физической реализации таких антенн с облучателями в виде рупоров. Минимально достижимый угловой разнос смежных лучей при еще приемлемых параметрах антенны составляет не менее 1,4–1,5 ширины диаграммы луча (определенной по уровню - 3 дБ), а при оптимальном облучении края зеркала не менее 2,0 ширин диаграммы направленности. Это условие приводит к тому, что при формировании непрерывной рабочей зоны многолучевых спутников связи типа HTS (например, на основе расстановки лучей в узлах равномерной гексагональной сетки) в составе бортовой антенной системы используется несколько (3–4) зеркальных многолучевых антенн (например спутники Ка-Sat, Viasat-1 и др.) Следует отметить, что постоянно идет поиск простых

решений, позволяющих снизить минимально достижимый угловой разнос смежных лучей (например, [7]). Кроме того, одним из наиболее известных других методов является замена каждого облучающего рупора группой облучающих рупоров (с меньшим раскрывом), образующих ФАР. Апертуры этих ФАР электрически пересекаются (то есть формируется гибридная зеркальная антенна). Однако эффективность таких решений и их физическая реализация для бортовых антенн коммерческих спутников связи типа HTS требует дополнительных научных исследований и сравнительных оценок достоинств и недостатков с учетом достигаемых электрических параметров (с учетом потерь и проблем широкополосности [8] в диаграммообразующих устройствах ФАР) и массогабаритных характеристик, поскольку высокая эффективность гибридных зеркальных антенн достигается при большом числе излучателей в облучающей ФАР [9].

Литература

1. Kyrgiazos A., Evans B., Thompson P. A feasibility study for a Terabit/s Satellite for European Broadband access // ICSSC. – 2012.
2. Shung-Wu Lee, Yahya Rahmat-Samii, Simple Formulas for Designing an Offset Multibeam Parabolic Reflector // IEEE Antennas and propagation – 1981. – Vol. 29, № 3. – P. 472– 478.
3. Maral G., Bousquest M. Satellite Communication Systems, 4th ed. // Wiley. – 2002.
4. Goldsmith P. F. Quasioptical systems // MSDH. – 1987. – P. 430.
5. Jull E. V. Aperture antennas and diffraction theory. – London, 1980. – P. 184.
6. Natale N., Nesti R. Front-end and Back-end in radioastron-omy. – URL: www.pos.sissa.it.
7. Chantalat R., Mondire T., Thvenot M., Jecko B., P. Dumon P. Multibeam Reflector Antenna with Integlaced Focal Feeds by Using a 1-D Dielectric EBG Resonator // URSI International Symposium on Electromagnetic Theory. – 2004. – P. 1050– 1052.
8. Классен В.И., Тоболев А.К., Шишлов А.В. Характеристики излучения гибридной зеркальной антенны в полосе частот // Радиотехника. – 1985. – № 9. – С. 69– 72.
9. Величко И.Л., Кривошеев Ю.А., Шишлов А.В. Гибридные зеркальные антенны с облучающими активными фазированными решетками // Антенны. – 2011. – № 10 (173). – С. 22-42.

Опубликовано: Журнал "Технологии и средства связи" #4, 2013
Посещений: 7130

Статьи по теме

• О фазированных антенных решетках Ka-диапазона на основе метаматериала. About metamaterial-based phased array antennas in the Ka-band
• Развитие современных мультисервисных сетей ШПД. Development of modern broadband multiservice networks
• Россия – один из наиболее перспективных рынков для спутникового вещания
• Развитие рынка VSAT-технологий в мире. Development of the VSAT-technology in the world
• Спутниковый ШПД – на волне успеха

Автор Анпилогов Валентин Романович Зам.ген.директора ЗАО "Висат-Теп" Всего статей:  56

Автор Александр Афонин аспирант МАИ Всего статей:  4

В рубрику "Спутниковая связь" | К списку рубрик  |  К списку авторов  |  К списку публикаций