В рубрику "Спутниковая связь" | К списку рубрик | К списку авторов | К списку публикаций
Чрезвычайно важным является знание фактической диаграммы направленности (ДН) любой ответственной антенной системы. Фактическая ДН определяет многие параметры антенно-фидерного устройства. Несоответствие фактической и расчетной ДН указывает на конструктивные ошибки при разработке антенной системы или на погрешности, возникающие при монтаже этой системы.
Поэтому большое внимание уделяется измерению характеристик больших стационарных антенн различными автоматизированными методами, в том числе облетными в условиях полигона.
Зарождение метрологического обеспечения в процессах разработки, изготовления и испытаний антенн следует отнести ко времени образования КБРП им. академика А.А. Расплетина (1970-е гг.).
При исследовании характеристик антенны РЛС в УКВ-диапазоне в СССР применялись измерительные комплексы на базе самолетов Ил-14 и Ан-12.
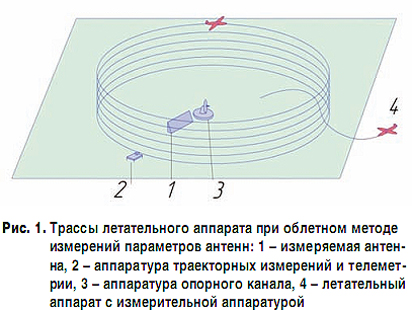
Конструкция антенного устройства, особенности и характеристики формируемой им диаграммы направленности определяли способ измерения диаграмм направленности в облетном методе. Для антенны, формирующей сложную диаграмму направленности в заданном секторе пространства при углах места не более 50–60 град., измерялись горизонтальные сечения диаграммы, при которых летательный аппарат совершал при постоянной на каждом проходе высоте круговой облет антенны. Удаление летательного аппарата от антенны по возможности выдерживалось близким к постоянному. Для получения высокой точности результатов при большом общем времени измерений применялся опорный канал.
Резюмируя в целом особенности облетного метода, применяемого для измерения характеристик крупноапертурных антенн в СССР, необходимо отметить, что большой объем необходимых измерений, а также работ по неавтоматизированной обработке результатов делали облетный метод одним из самых технически сложных [1].
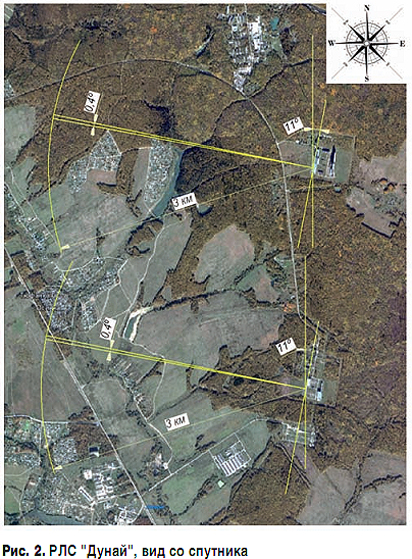
Наша работа посвящена вопросам метрологического обеспечения крупногабаритных стационарных антенн, и главной задачей является решение проблем метода, применявшегося в СССР.
Специфика данного метода требует внедрения максимального уровня автоматизации всех этапов работ – от управления полетами, проведения измерений и регистрации данных измерений до обработки информации и построения диаграммы направленности антенны.

Главным достоинством современных БПЛА по сравнению с пилотируемыми летательными аппаратами является то, что они позволяют избежать потерь летного состава и решать задачи при меньших экономических затратах. К тому же отсутствие человека на борту БПЛА позволяет автоматизировать процесс измерений на всех этапах, снять многие конструктивные ограничения, увеличить эксплуатационную надежность, снизить взлетную массу.
Далее расмотрим предлагаемый метод на примере активных фазированных антенных решеток.
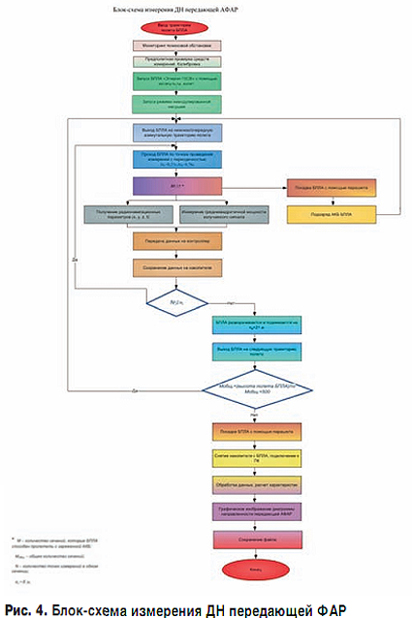
Объектами измерений являются передающая и приемная АФАР с размерами апертуры соответственно 100х20 и 100х50 м (длина х высота).
Размеры апертур позволяют сделать вывод о форме исследуемой диаграммы направленности: в горизонтальном сечении узкая ДН, в вертикальном – широкая ДН, то есть ДН будет иметь "веерную" (многолучевую) форму.
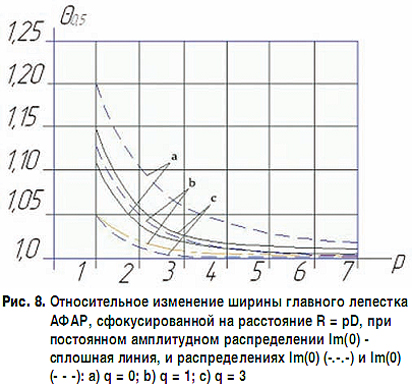
Учитывая наибольший размер апертуры РЛС, расстояние дальней зоны будет существенным. Поэтому для сокращения эксплуатационных затрат и организационных сложностей предлагается использовать метод перефокусировки АФАР на 3 км.
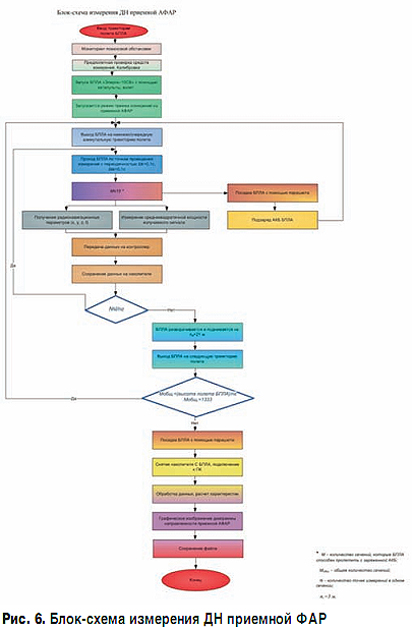
В работе рассмотрены вопросы высокоточного навигационного обеспечения на основе спутниковой радионавигации, ошибки измерений и источники возникновения погрешностей, программное и аппаратное обеспечение комплекса, наземная инфраструктура, а также организационно-технические вопросы эксплуатации измерительного комплекса. В том числе параметры облета, вопросы регистрации и постобработки результатов измерений.
Для измерения характеристик приемной и передающей антенн используются различные алгоритмы и бортовое оборудование. Измерения значений плотности потока мощности излучения передающей АФАР будут производиться в узлах облетной сетки на квазиоптимальном расстоянии от источника. При измерении приемной АФАР используется подобная облетная сетка, но источником будет являться бортовой излучатель. А измерения будут производиться приемником самой АФАР.

Глобальные координаты, получаемые с навигационных спутников, регистрируются на борту БПЛА с временной меткой.
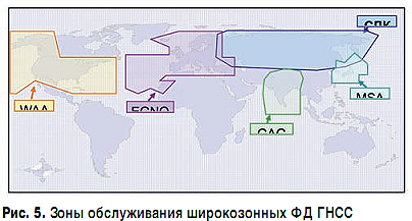
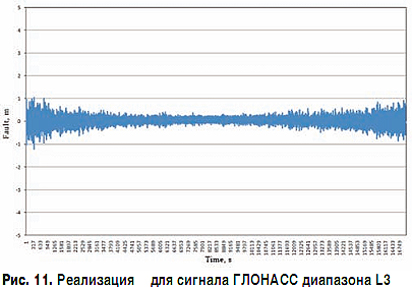
Задачу высокоточного измерения положения измерительного зонда в пространстве мы предлагаем решить с помощью широкозонной дифференциальной ГЛОНАСС-радионавигации с использованием корректирующей информации, передаваемой системой дифференциальной коррекции и мониторинга (СДКМ) в навигационном диапазоне (~1575 МГц) в структуре навигационных радиосигналов GPS в формате SBAS через геостационарные спутники серии "Луч-5".
В результате проведенных исследований был сделан вывод, что погрешность в результатах измерений вызывается 4 причинами:
1. Ошибки, связанные с фокусировкой АФАР.
Сделанные расчеты свидетельствуют о хорошей потенциальной точности метода уже при измерениях на расстояниях более 2–3 размеров раскрыва.
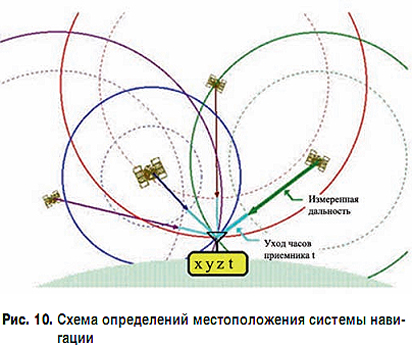
2. Ошибки, связанные определением глобальных координат. Во-первых, это условия распространения радиоволн. Волне, пробиваясь из открытого космоса на Землю, приходится проходить через разные слои атмосферы, где она преломляется, как показано на рисунке.
Во-вторых, точность определения координат спутника напрямую связана с точностью эфемерид. Эфемериды придумывают не сами спутники, они загружаются на спутник с наземных контрольных станций, примерно раз в сутки. Кроме начальных погрешностей, они еще "портятся с возрастом". Сюда же условно можно отнести уход бортовых часов спутника.
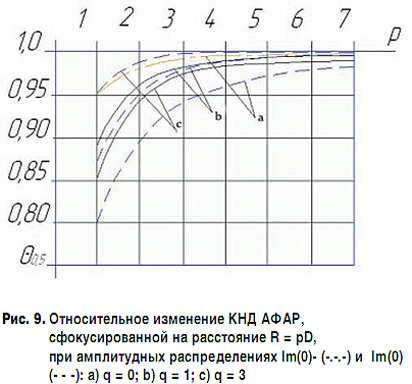
На основе проведенных расчетов показана возможность достижения следующих точностей координатно-скоростных определений БПЛА не хуже ~ 1–1,5 м по вектору местоположения и не хуже ~ 1,5–2 см/с по вектору скорости полета.
3. Ошибки, связанные с измерением мощности излучения:
4. Ошибки, возникающие в процессе постобработки данных измерений:
Совершив облет, БПЛА возвращается в точку старта и совершает посадку на парашюте. Затем данные с бортового накопителя обрабатываются по специальным алгоритмам вычислительным узлом, расположенным в наземном пункте управления (НПУ).
НПУ представляет собой специально подготовленное транспортное средство, предназначенное для управления БПЛА, контроля полета, транспортирования оборудования и обслуживающего его персонала, обеспечения бесперебойного функционирования оборудования как в движении, так и на стоянке.
Фургон имеет 2 зоны: салон (аппаратный отсек) и отсек для размещения мачтового и антенно-фидерного оборудования (антенный отсек). На крыше фургона устанавливается антенно-фидерная система, которая закрывается съемным радиопрозрачным куполом.
В рабочем отсеке (салоне) смонтированы места операторов, места размещения аппаратуры и оборудования, места размещения антенных и иных систем, система электропитания, система жизнеобеспечения и безопасности. В антенном отсеке, кроме мест для размещения мачтового и антенно-фидерного оборудования, имеются места для отдыха операторов.
Результатом обработки будут являться формализованные фактические ДН (объемная ДН, различные сечения по выбору оператора, картографические проекции, параметры АФАР, рассчитанные по ДН (ЭИИМ, шумовая добротность)). В результате мы с требуемой точностью сможем сказать, каким образом фактическая ДН отличается от расчетной.
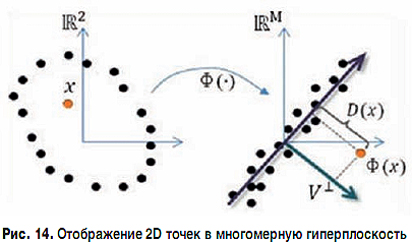
Для визуализации измеренных данных, которые представляют собой после обработки некий массив точек в трехмерном пространстве, нужно построить поверхность, состоящую из полигонов, в простейшем случае представляющих собой треугольники.
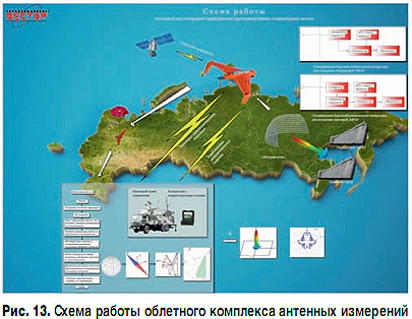
Используем алгоритмы, описанные в публикациии израильских ученых Поранна и Готсмана "Восстановление трехмерной поверхности с использованием обобщенной функции расстояния" [2].
Радиальная базисная функция (RBF) - функция, принимающая вещественные значения и зависящая от дистанции от какой-либо выбранной точки c, называемой центром, (x, c) = (||x - c||), где x, c - векторы, || || - Евклидово расстояние. Простейшим примером является полигармонический сплайн степени 1: (r) = r, где r - Евклидово расстояние.
Рассмотрим вектор следующего вида:
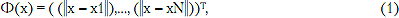
где . N
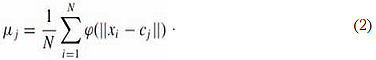
Этот вектор получается отображением вектора x из пространства двух или трех измерений в M-мерное пространство. M - это число центров, выбранных из входного массива точек. Алгоритм выбора не описан в работе [2], но существует публикация Кононыхина [3] для отбрасывания наименее важных центров. Если входных точек немного (несколько сотен), можно в качестве центров выбрать все входные точки. Если точек много (тысячи, десятки и сотни тысяч), возникнут сложности при вычислении матриц соответствующего размера, поэтому число центров в таком случае нужно ограничивать.
Составим матрицу следующего вида:

где i - номер строки, j - номер столбца.
В математической статистике и теории вероятностей используется так называемая матрица ковариации. В данном методе построения поверхности строится матрица ковариации для вектора (x) так, как если бы его координаты были случайными числами. Распределение векторов x представляет собой некоторый неупорядоченный массив.
Матрица ковариации выглядит следующим образом:

Матрица ковариации необходима для вычисления расстояния Махаланобиса [4]. Расстояние Махаланобиса между произвольным вектором (x) и массивом векторов (x), вычисленных для входных точек, обобщает понятие Евклидова пространства и учитывает форму эллипсоида матрицы ковариации.
Путем сингулярного разложения матрицы ковариации получаем следующую формулу для вычисления расстояния Махаланобиса:
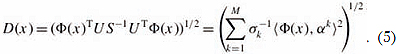
Здесь k - столбцы матрицы U (собственные векторы матрицы ковариации), k - собственные значения матрицы ковариации.
Поранн показал, что можно использовать несколько наименьших собственных пар матрицы - 1, а не все:
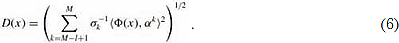
Расстояние Махаланобиса для точек, лежащих вблизи от предполагаемой поверхности, будет наименьшим. Используется отрицательное расстояние Махаланобиса.
На рис. 15 красным цветом обозначены минимальные отрицательные расстояния Махаланобиса, а темно-синим - наибольшие. Видно, что в области, ограниченной контуром руки, есть локальный минимум. И за областью контура тоже существуют другие локальные минимумы.
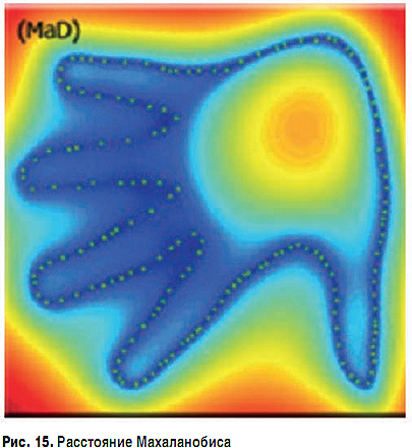
Паренн в своей работе использует алгоритм водораздела, в котором предлагается рассматривать минимумы как глубокие участки бассейнов. При их постепенном наполнении в определенный момент вода из одного бассейна перельется в другой [2].
Для выделения искомой поверхности разобьем параллелепипед, ограничивающий входной массив точек, на маленькие кубы и в центре каждого вычислим расстояние Махаланобиса и умножим его на - 1.
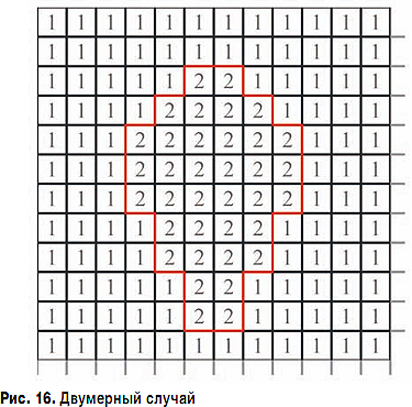
Каждый из кубов будет стягиваться к какому-то локальному минимуму отрицательного расстояния Махаланобиса. На рис. 16 показан двумерный случай. Ограничивающий прямоугольник разбит на квадраты. Каждый квадрат своим значением расстояния Махаланобиса относится к какому-то локальному минимуму. Каждый квадрат имеет 4 смежных квадрата, с каждым из которых он разделяет общее ребро. Те ребра, которые разделяют квадраты, относящиеся к разным минимумам, образуют искомую ломаную, аппроксимирующую предполагаемую кривую, огибающую массив входных точек. Для трехмерного случая рассуждения аналогичны.
Следует отметить, что алгоритмы и методики, описанные в статье, справедливы не только для задач измерения и подтверждения характеристик широкого спектра крупноапертурных стационарных антенн, но и для пространственного анализа электромагнитного поля, в том числе для анализа сетей сотовой связи 2G/3G/4G.
Литература
Опубликовано: Журнал "Технологии и средства связи" #1, 2014
Посещений: 8349
Статьи по теме
Автор
| |||
Автор
| |||
Автор
| |||
Автор
| |||
В рубрику "Спутниковая связь" | К списку рубрик | К списку авторов | К списку публикаций