В рубрику "Спутниковая связь" | К списку рубрик  |  К списку авторов  |  К списку публикаций

Оценка пульсации группового времени запаздывания в линии передачи и ее влияние на передачу цифровой информацииEvaluation group delay ripple in the transmission line and its influence on digital transmission

Валентин
Анпилогов

Заместитель генерального директора ЗАО "ВИСАТ-ТЕЛ", к.т.н.

Valentin
Anpilogov Deputy General Director JSC VSAT-TEL, Dr.Sc.

Галина
Головченко

Доцент МИРЭА, к.т.н.

Galina
Golovchenko

Associate professor in Moscow State Institute of Radio Engineering, Electronics and Automation&, Dr.Sc.

Групповое время запаздывания (ГВЗ) характеризует время распространения сигнала, в данном случае – время распространения сигнала в линии передачи (предполагается, что в линии передачи отсутствуют активные элементы). Естественно, если время распространения постоянно в полосе частот спектра сигнала, то сигнал передается без искажений. Очевидно, что обеспечить постоянство ГВЗ в широкой полосе частот практически невозможно. Неравномерность ГВЗ – один из параметров линии передачи любой физической природы. В случае если в линии передачи отсутствуют неоднородности, то неравномерность ГВЗ имеет монотонный характер, а ее величина в заданной полосе частот определяется дисперсионными свойствами линии передачи. Наличие неоднородностей в линии передачи принципиально изменяет характер неравномерности ГВЗ, а именно: добавляется пульсирующая составляющая ГВЗ. Эта составляющая обусловлена взаимодействием неоднородностей, распределенных по длине линии передачи. Это взаимодействие обусловлено возникновением отраженных и переотраженных сигналов. Величина и период пульсации ГВЗ зависят от величины неоднородностей и расстояний между взаимодействующими неоднородностями.

Наличие неравномерности ГВЗ в полосе частот спектра сигнала приводит к так называемым линейным искажениям. Начиная примерно с 1960-х гг. этим вопросам было посвящено много исследований, особенно применительно к влиянию неравномерности ГВЗ в СВЧ-трактах радиорелейных станций связи с аналоговыми видами модуляции и частотным разделением каналов. Показано, что влияние НГВЗ на передачу информации может быть значительным (проявляется в образовании переходных помех между каналами) и зависит от характера изменения неравномерности ГВЗ в полосе частот (параболическая, линейная или пульсирующая функция). Позднее аналогичные исследования были выполнены и для цифровых видов модуляции (влияние НГВЗ проявляется в межсимвольной интерференции). Однако эти исследования не имеют завершенного уровня, что отчасти объясняется разнообразием применяемых сигнально-кодовых конструкций и различным влиянием частотной зависимости неравномерности ГВЗ на конечный результат.

Следует отметить, что частотную зависимость ГВЗ, обусловленную дисперсионными свойствами линии передачи, всегда можно скомпенсировать за счет использования корректоров ГВЗ. Пульсирующая составляющая в большинстве своем имеет случайный характер. Ее компенсация с использованием корректоров ГВЗ невозможна или по крайней мере очень затруднительна. Соответственно подходы к оценке и прогнозированию пульсации ГВЗ в неоднородной линии передачи и оценке ее влияния на передачу информации имеют отдельное самостоятельное значение. Существует как минимум два предельных случая. Первый предполагает наличие двух неоднородностей в линии передачи [1-4] на расстоянии L друг от друга, что отвечает часто встречающейся на практике ситуации, которая связана с рассогласованием на входе и выходе линии передачи. Второй случай предполагает множество малых неоднородностей в линии передачи, распределенных по ее длине [5]. Промежуточным является вариант, который предполагает наличие малого числа неоднородностей [6], но более двух. Каждый из вариантов предполагает в качестве основного параметра модуль коэффициента отражения (по напряжению) от неоднородности. Соответственно можно установить взаимосвязь между величиной пульсации ГВЗ и модулем коэффициента отражения (или КСВ (н)) на входе линии передачи [2, 7, 8].

Две неоднородности

Наличие двух неоднородностей на входе и выходе линии передачи является простейшим случаем, но очень полезным для практических целей. Эта задача рассмотрена в [1, 2] применительно к условию относительно малых неоднородностей (коэффициент отражения ГГГ2 < 0,1). Функция ГВЗ (т3) в полосе частот приобретает пульсирующий характер [2]:

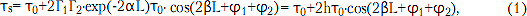
где Г₁ и Г₂ - модули коэффициента отражения неоднородностей по напряжению (слабо зависят от частоты), расположенных в линии передачи на расстоянии L друг от друга (например, на входе и выходе);

φ₁ и φ₂ - фазы коэффициентов отражения от неоднородностей в месте их расположения (слабо зависят от частоты);

α - погонное затухание в линии передачи (неп/м);

L - расстояние между неоднородностями (м);

β = 2π/λ - фазовая постоянная в регулярной линии передачи;

λ - длина волны в регулярной линии передачи (м);

T₀ = L/Vr - групповое время запаздывания в регулярной линии передачи (предполагается, что в анализируемой полосе частот практически постоянно);

Vr - групповое время запаздывания в регулярной линии передачи.

Пульсация ГВЗ имеет характер, отвечающий функции cos(2βL), периодичность которой соответствует

Пульсация ГВЗ в полосе частот более Δf достигает величины

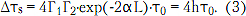
С другой стороны, можно показать, что модуль коэффициента отражения на входе линии передачи (при относительно малом затухании и Δτs связаны простым соотношением [2]

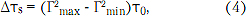
где Гmах и Гmin - максимальное и минимальное значение модуля коэффициента отражения на входе линии передачи в полосе частот.

Соответственно оценки (1-4) справедливы в полосе частот не менее Af для относительно малых неоднородностей, которые и имеют место в практически значимых случаях.

Если Г₁ и Г₂ не отвечают условию малости, то следует учитывать все возможные пути отражений и переотражений сигнала. Применительно к этому условию пульсация ГВЗ определяется выражением [4]:

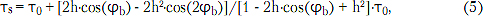
где φb = - 2βL + φ₁ + φ₂ - текущая фаза (знаки несущественны).

Соотношение (5) совпадает с (1) при условии малости неоднородностей, но в отличие от (1) более интересно для дальнейшего анализа скорости распространения сигнала в неоднородной линии передачи. Особо отметим, что величина пульсации ГВЗ может иметь как знак плюс, так и минус в зависимости от радиочастоты сигнала.

Множество малых неоднородностей

В реальной линии передачи число неоднородностей может быть очень большим. Причем неоднородности в подавляющем большинстве случаев малы и распределены случайно. Последнее обстоятельство переводит задачу в плоскость вероятностного решения. В [5] для ее решения принято распределение N+1 неоднородностей по длине линии передачи:

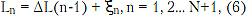
где Ln - расстояния от входа линии передачи до n-й неоднородности;

ξп - случайная величина, распределенная равномерно на интервале [0; AL];

ΔL = L/N - среднее расстояние между неоднородностями, где L - общая длина линии передачи.

В [5] показано, что пульсация ГВЗ в данном случае соответствует центрированному относительно т0 случайному процессу, который можно считать нормальным уже при п > 8 и стационарным в точном смысле. Такой процесс можно отождествить с совокупностью случайных величин, которые не являются коррелированными, если сечения этого процесса отстоят друг от друга по частоте на величину

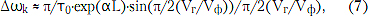
Vr/Vф - отношение групповой скорости к фазовой скорости в линии передачи.

В заданной полосе частот Δω - число некоррелированных сечений

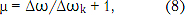
что определяет многомерную функцию распределения пульсации ГВЗ для заданной полосы частот Δω. Интегральная функция распределения в этом случае соответствует нормированной функции Лапласа (интеграл вероятностей) в степени μ.

В результате в [5] получено, что величина пульсации ГВЗ в полосе частот Δω с заданной вероятностью Ро не превысит величины

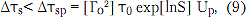
где [Г₀²] - среднее значение квадратов модулей коэффициентов отражений от отдельных неоднородностей (примерно равно среднему значению произведений коэффициентов отражений двух любых взаимодействующих неоднородностей ГiГк при условии их примерного равенства);

InS - коэффициент, определяющий максимально достижимую пульсацию ГВЗ для известного числа неоднородностей п и затухания <xL в линии передачи (рис. 1);

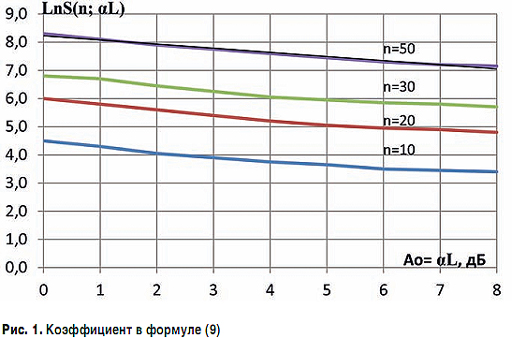
Up - значение, соответствующее вероятности Р₀ = (Рμ)^1/μ интеграла вероятности.

Для упрощения получения конечного результата целесообразно воспользоваться законом трех сигм. В результате можно принять, что величина пульсации ГВЗ с вероятностью 0,997 = (Рμ)^1/μ лежит в интервале значений, соответствующих Up = 3. Очевидно, что при необходимости, воспользовавшись (7) и (8), можно оценить и полосу частот Δω, в которой пульсация ГВЗ достигнет практически своего максимального значения.

В (5) отмечено, что чем больше число неоднородностей, тем меньше конечный результат зависит от функции их распределения.

В случае большого числа малых неоднородностей можно установить функциональную взаимосвязь между пульсацией модуля коэффициента отражения на входе линии передачи и пульсаций ГВЗ. Так, в [6, 7] показано, что

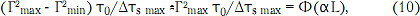
где Ф(αL) - при Г²max >> Г²min изменяется от 1,35 до 0,75 в интервале αL от 0 до 7 дБ.

При этом значение модуля максимального коэффициента отражения Гтах на входе линии передачи, как следует из [6, 7], приближенно можно записать в виде

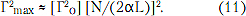
Представленные соотношения имеют достаточно большое практическое значение. Например, используя (11) и (10 или 9), сформулировать требования к качеству коаксиального кабеля, то есть нормировать допустимое число неоднородностей N+1 в зависимости от допустимой величины пульсации ГВЗ или КСВ(н) на входе отрезка заданной строительной длины L при известном погонном затухании сх (неп/м). В качестве исходного параметра может служить величина отклонения волнового сопротивления, публикуемая производителем, которая однозначно определяет значение [Г20]. Такие особые требования целесообразны для кабелей, предназначенных для передачи высокоскоростных потоков цифровой информации с использованием многопозиционной модуляции.

Малое число малых неоднородностей

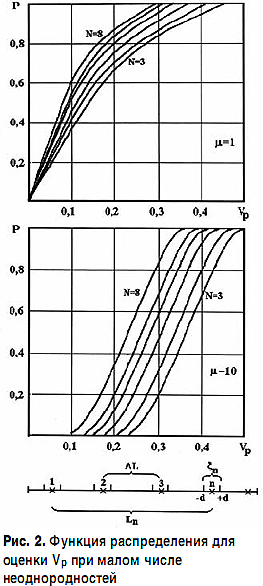
Этот случай выделяется тем, что функция распределения случайной величины, то есть пульсации ГВЗ, уже не отвечает нормальному закону. Для упрощения задачи принято распределение неоднородностей по длине линии передачи [9]

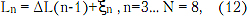
где ξn – случайная величина, распределенная равномерно на интервале [-d;+d] и d<< ΔL = L/N.

То есть распределение неоднород-ностей (12) "менее случайно". Например, эта задача близка к той, которая решалась в [10] при оценке пульсации ГВЗ в тракте РРС, собранном из примерно равных отрезков волновода, где неоднородности определены точностью стыковки фланцев.

Для этого случая принята специальная функция, представленная в [8]. В итоге в [9] получено соотношение, которое приведено ниже с унифицированными обозначениями параметров как в формуле (9):

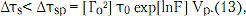
где lnF – коэффициент (рис. 3), подобный lnS (рис. 1).

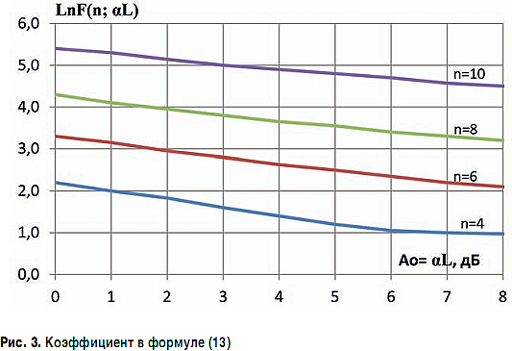
В отличие от (9) уже нет возможности использовать табулированные значения интеграла вероятности, поэтому данные для вычислений приведены на рис. 2 для фиксированной частоты (μ=1) и в полосе частот (μ=10).

Влияние пульсации ГВЗ

В ряде работ отмечается, что неравномерность ГВЗ может иметь сильное влияние на достоверность передачи цифровой информации [11, 12]. Это проявляется в деградации Еb/No, что ограничивает предельные возможности скорости передачи информации [13]. Степень деградации Еb/No при наличии пульсации ГВЗ в спектре сигнала оценена для ряда видов цифровой модуляции в [14–16]. Совокупные данные для этого случая представлены в таблице.

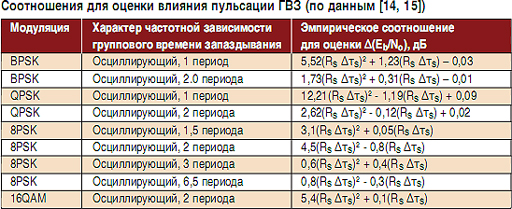
Анализ данных показывает, что с увеличением числа периодов влияние пульсации ГВЗ снижается, но для сложных видов многопозиционных сигналов влияние пульсации ГВЗ увеличивается и может быть значительным. Эти результаты (таблица) не имеют завершенного вида и требуют дальнейших теоретических и экспериментальных исследований для широкого класса сигнальнокодовых конструкций.

Компенсация пульсации ГВЗ

Компенсация пульсации ГВЗ, вызванной неоднородностями в линии передачи, с использованием корректоров ГВЗ (как это производится для линейной и параболической зависимости неравномерности ГВЗ) практически невозможна. В случае наличия значительных неоднородностей на входе линии передачи эффективным способом является установка невзаимного устройства, например, как показано на рис. 4, с использованием циркулятора в режиме вентиля.

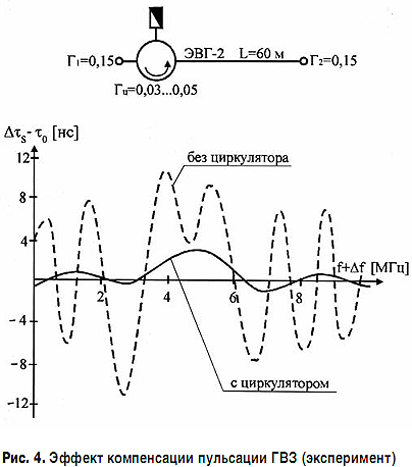
Если неоднородности распределены по всей линии передачи, то значительная компенсация пульсации ГВЗ достигается путем установки в ее середине циркулятора и фазовращателя. Наличие циркулятора снижает пульсацию ГВЗ в разы, а подбором фаз можно обеспечить практически полную компенсацию пульсации ГВЗ.

Парадокс – групповая скорость больше скорости света

Если внимательно посмотреть на соотношение (1), то очевидно, что пульсация ГВЗ имеет синусоидальный характер. При этом общая задержка распространения сигнала на отдельных частотах более задержки в регулярной линии передачи. Однако на других частотах становится меньше, то есть как бы групповая скорость больше, чем в регулярной линии передачи. Это можно было бы отнести к принятому приближению, но и соотношение (5), свободное от этого приближения малости неоднородностей, дает аналогичный результат. Его анализ показывает, что групповая скорость вообще может стать нулевой, правда в этом случае и распространения сигнала не будет, так как величины модуля коэффициента отражения для неоднородностей будут достигать единицы (Г₁Г₂ = 1) и коэффициент передачи соответственно равен нулю.

Но есть и промежуточные значения в области частот ωi, в которых общая задержка в неоднородной линии передачи τs (ωi) < τ0. Это иллюстрируется на рис. 5.

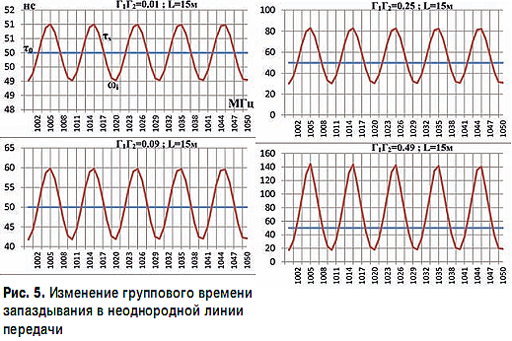
В качестве примера для конкретности принята линия передачи длиной 15 м без внутреннего заполнения и с тепловыми потерями, близкими к нулю, на входе и выходе которой имеются неоднородности (красная линия показана τs (ω)), если неоднородности отсутствуют, то групповая скорость распространения практически равна скорости света Vг = С (синим показана групповая задержка в регулярной линии передачи). При наличии неоднородностей групповое время запаздывания в линии передачи приобретает пульсирующую составляющую, при этом получается парадоксальный эффект:

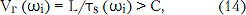
где τs (ωi) – групповое время запаздывания в интервале Δω/ωi <<1 (рис. 5);

C – скорость распространения света, Vг (ωi) – групповая скорость распространения электромагнитной волны в интервале частот Δω/ωi <<1.

Следует отметить, что с увеличением Г1Г2 вносимые потери на частотах ωi увеличиваются, достигая бесконечности при Г1Г2 = 1.

В известной сегодня научной литературе существует два противоположных мнения. Первая многочисленная группа исследователей не допускает возможности Vг > C, вторая – менее многочисленная – уверена, что такой эффект имеет место (тахионы, нейтрино и запутанные частицы, распространение в парах цезия, в активных средах и т.п.). Основное расхождение взглядов связано с интерпретацией понятия "групповая скорость" распространения сигнала (волны) и принципа причинности. Для полноты картины отметим противоположные по своим взглядам работы [17–21]. Более того, в ряде работ утверждается возможность достижения отрицательного значения ГВЗ в активных средах (радиотехнических устройствах). Видимо, это ошибочная терминология, связанная с игнорированием регулярной составляющей времени запаздывания (в нашем случае τ0).

Выводы

Представленные выше соотношения позволяют оценить величину пульсации ГВЗ в полосе частот спектра сигнала при его распространении в неоднородной линии передачи любой физической природы. Эта оценка может быть выполнена как расчетным путем, так и путем пересчета результатов измерения коэффициента отражения на входе линии передачи. Эти данные позволяют оценить влияние пульсации ГВЗ на передачу информации в линии связи (см. таблицу). Анализ влияния пульсации ГВЗ на качество передачи цифровой информации показывает, что деградация Eb/N0 может иметь достаточно высокий уровень. В этом случае возможны варианты компенсации пульсации ГВЗ с использованием невзаимных, хорошо согласованных устройств в составе линии передачи.

В процессе анализа соотношений, представленных выше, получен результат, который говорит о том, что на определенных частотах (в области частот, где коэффициент отражения достигает максимумов) может наблюдаться парадоксальный эффект – групповая скорость передачи в неоднородной линии превышает скорость распространения света. Однако групповое время запаздывания всегда остается положительной величиной. Парадокс заключается в том, что в окрестности этих частот потенциально можно передать информацию со скоростью, превышающей скорость света в вакууме. Более подробное объяснение этого эффекта и его экспериментальное подтверждение или опровержение – тема отдельной статьи. n

Литература

1. Beatty Robert W., Otoshi, Tom Y. Effect of Discontinuities on the Group Delay of a Microwave Transmission Line // IEEE Transactions on Microwave Theory and Techniques.– 1975, Vol. 23. – P. 919–923.
2. Анпилогов В.Р. Групповое время запаздывания протяженной линии передачи с учетом потерь и неоднородностей при одноволновой работе / В.Р. Анпилогов, Г.С. Головченко, А.П. Сахаров // Техника средств связи. – 1976. – Вып. 1. – С. 171–176. – Серия: ТРС.
3. Анпилогов В.Р. Групповое время запаздывания протяженного СВЧ-тракта / Тезисы докладов IV Всесоюзной конференции по антенно-фидерным трактам для радиосвязи, радиовещания и телевидения. – Москва, 1976. – 4–7 января.
4. Eskandari A.R., Mohammadi L. Group Delay Variations in Wideband Transmission Lines: Analysis and Improvement // International Journal of Soft Computing and Engineering (IJSCE). – 2011, Vol. 1. – ISSN: 2231-2307.
5. Анпилогов В.Р., Николаев В.А. Статистическая оценка величины осцилляции группового времени запаздывания СВЧ-тракта в полосе частот // Техника средств связи. – 1978. – Вып. 1. – С. 103–109. – Серия ТРС.
6. Анпилогов В.Р. Упрощенный способ оценки величины осцилляции времени запаздывания в заданной полосе частот / Тезисы докладов IV Всесоюзной конференции "Метрология в радиоэлектронике". – 1978. – 12–14 сентября. – С. 84–86.
7. Анпилогов В.Р., Головченко Г.С. Взаимосвязь пульсации группового времени запаздывания и коэффициента отражения на входе неоднородной линии передачи // Антенны. – 1999. – Вып. 2 (43).
8. Левин Б.Р. Теория случайных процессов и ее применение в радиотехнике. – М.: Советское радио, 1957.
9. Анпилогов В.Р. Пульсация группового времени запаздывания СВЧ-тракта с малым числом неоднородностей // Электромагнитные волны и электронные системы. – 1997. – Т. 2, № 6.
10. Тартаковский Л.С. Статистическое исследование неравномерности группового времени запаздывания в волноводных трактах магистральных РРД // Электросвязь. – 1977. – № 6. – С. 39–43.
11. Spilker J. J. Digital communications by satellite, Prentice Hall PTR Upper Saddle River. – USA: NJ, 1977. – ISBN:0132141558.
12. Спутниковая связь и вещание / Справ. под ред. Л.Я. Кантора, 3-е изд. – М.: Радио и связь, 1997. – 528 с.
13. Анпилогов В.Р., Афонин А.А. О предельно достижимой скорости цифрового потока в системах связи и вещания // Технологии и средства связи. Спецвыпуск "Спутниковая связь и вещание". – 2011. – № 6-2. – С. 92–95.
14. Back S., Weigel M. Degradation of digital satellite signals by group delay, Globecomm System Inc & EFDATA Corporation // Appeared In world Broadcast News. – 1999. – November.
15. Azizzadeh A., Mohammadi L. Degradation of BER by Group Delay in Digital Phase Modulation / The Fourth Advanced International Conference on Telecommunications (AICT 2008), Athens, Greece, June 8–13. – 2008. – Р. 350– 354.
16. Eskandari A.R. A Novel Method for Analyzing & Predicting of Group Delay Variations in Wideband Transmission Lines / А.R. Eskandari, L. Mohammady, B. Eliasi // IEEE International Workshop on Radio-Frequency Integration Technology. – RFIT, 2007.
17. Давидович М.В. Прохождение сигналов через фильтр с поглощением и отрицательное время задержки // Журнал технической физики. – 2012. – Т. 82, вып. 3. – С. 15–223.
18. Давидович М.В. О парадоксе Хартмана, туннелировании электромагнитных волн и сверхсветовых скоростях // Успехи физических наук. – 2009. – Т. 179 – С. 443–446.
19. Бухман Н.С. О реальности сверхсветовой групповой скорости и отрицательности времени задержки волнового пакета в диспергирующей среде // Журнал технической физики. – 2002. – Т. 72, вып. 1. – С. 136–138.
20. Бухман Н.С., Бухман С.В. Об отрицательном времени задержки узкополосного сигнала при прохождении через резонансный фильтр поглощения // Известия высших учебных заведений. Радиофизика. – 2004. – Т. 47, № 1. – С. 75–84.
21. Bukhman N.S., Bukhman S.V. On the Negative Delay Time of a Narrow-Band Signal as It Passes Through the Resonant Filter of Absorption // Radiophysics and Quantum Electronics. – 2004. – Т. 47, № 1. – С. 68–76.

Опубликовано: Журнал "Технологии и средства связи" #2, 2014
Посещений: 11434

Автор Анпилогов Валентин Романович Зам.ген.директора ЗАО "Висат-Теп" Всего статей:  56

Автор Галина Головченко Доцент МИРЭА, к.т.н. Всего статей:  1

В рубрику "Спутниковая связь" | К списку рубрик  |  К списку авторов  |  К списку публикаций