ąÆ čĆčāą▒čĆąĖą║čā "ąĪą┐čāčéąĮąĖą║ąŠą▓ą░čÅ čüą▓čÅąĘčī" | ąÜ čüą┐ąĖčüą║čā čĆčāą▒čĆąĖą║ | ąÜ čüą┐ąĖčüą║čā ą░ą▓č鹊čĆąŠą▓ | ąÜ čüą┐ąĖčüą║čā ą┐čāą▒ą╗ąĖą║ą░čåąĖą╣
ąÆą┐ąŠčüą╗ąĄą┤ąĮąĄąĄ ą▓čĆąĄą╝čÅ ą┐ąŠčÅą▓ąĖą╗ąĖčüčī čüčĆą░ąĘčā ąĮąĄčüą║ąŠą╗čīą║ąŠ ąĮąŠą▓čŗčģ ą┐čĆąŠąĄą║č鹊ą▓ ą▓čüąĄą╝ąĖčĆąĮąŠą│ąŠ čüą┐čāčéąĮąĖą║ąŠą▓ąŠą│ąŠ ąśąĮč鹥čĆąĮąĄčéą░ ŌĆō ą░ą╝ąĄčĆąĖą║ą░ąĮčüą║ąĖą╣ ą┐čĆąŠąĄą║čé ą║ąŠą╝ą┐ą░ąĮąĖą╣ Google ąĖ SpaceX, ą▒čĆąĖčéą░ąĮčüą║ąĖą╣ OneWeb ąĖ čĆąŠčüčüąĖą╣čüą║ąĖą╣ Yaliny. ąÜą░ąČą┤ą░čÅ ą│čĆčāą┐ą┐ąĖčĆąŠą▓ą║ą░ ą┐čĆąĄą┤čüčéą░ą▓ą╗čÅąĄčé čüąŠą▒ąŠą╣ ą┤ąĄčüčÅčéą║ąĖ ą╝ą░ą╗čŗčģ čüą┐čāčéąĮąĖą║ąŠą▓. ą¦č鹊ą▒čŗ ą┐ąŠą┤ąŠą▒ąĮčŗąĄ ą║ąŠą╝ą╝ąĄčĆč湥čüą║ąĖąĄ ą┐čĆąŠąĄą║čéčŗ ą╝ąŠą│ą╗ąĖ čŹčäč乥ą║čéąĖą▓ąĮąŠ čĆą░ą▒ąŠčéą░čéčī, ą▓čŗčłąĄą┤čłąĖąĄ ąĖąĘ čüčéčĆąŠčÅ ą░ą┐ą┐ą░čĆą░čéčŗ ąĮčāąČąĮąŠ ą▒čāą┤ąĄčé ąŠą┐ąĄčĆą░čéąĖą▓ąĮąŠ ąĘą░ą╝ąĄąĮčÅčéčī ąĮąŠą▓čŗą╝ąĖ. ąŁč鹊 ąĮąĄ čüą╝ąŠą│čāčé čüą┤ąĄą╗ą░čéčī čéčĆą░ą┤ąĖčåąĖąŠąĮąĮčŗąĄ ą▒ąŠą╗čīčłąĖąĄ čĆą░ą║ąĄčéčŗ, ą┐ąŠčüą║ąŠą╗čīą║čā ą▓čŗą▓ąŠą┤ąĖčéčī ą╗ąĖčłčī ąŠą┤ąĖąĮ ą╝ą░ą╗čŗą╣ čüą┐čāčéąĮąĖą║ ą▒ąŠą╗čīčłąŠą╣ čĆą░ą║ąĄč鹊ą╣ ŌĆō čŹč鹊 ą░ą▒čüčāčĆą┤ąĮąŠ ą┤ąŠčĆąŠą│ąŠ. ąĢčüą╗ąĖ ąČąĄ ąČą┤ą░čéčī ą┐ąŠą┐čāčéąĮąŠą│ąŠ ąĘą░ą┐čāčüą║ą░ ąĮą░ ą▒ąŠą╗čīčłąŠą╣ čĆą░ą║ąĄč鹥, č鹊 čåąĄąĮą░ čüčéą░ąĮąĄčé ąŠč湥ąĮčī ą┐čĆąĖą▓ą╗ąĄą║ą░č鹥ą╗čīąĮąŠą╣, ąĮąŠ ąĮąĖ ąŠ ą║ą░ą║ąŠą╣ ąŠą┐ąĄčĆą░čéąĖą▓ąĮąŠčüčéąĖ čāąČąĄ ą│ąŠą▓ąŠčĆąĖčéčī ąĮąĄ ą┐čĆąĖą┤ąĄčéčüčÅ. ą¤ąŠčŹč鹊ą╝čā ą╝ąĮąŠąČąĄčüčéą▓ąŠ čüčéą░čĆčéą░ą┐ąŠą▓ ą▓ ą╝ąĖčĆąĄ ą┐čŗčéą░čÄčéčüčÅ čĆą░ąĘčĆą░ą▒ąŠčéą░čéčī čüą▓ąĄčĆčģą╗ąĄą│ą║čāčÄ čĆą░ą║ąĄčéčā, ą║ąŠč鹊čĆą░čÅ ą╝ąŠą│ą╗ą░ ą▒čŗ ąŠą┐ąĄčĆą░čéąĖą▓ąĮąŠ ą▓čŗą▓ąŠą┤ąĖčéčī ą▓ ą║ąŠčüą╝ąŠčü čüą┐čāčéąĮąĖą║ąĖ ą╝ą░čüčüąŠą╣ ąŠčĆąĖąĄąĮčéąĖčĆąŠą▓ąŠčćąĮąŠ ąŠčé 1 ą┤ąŠ 200 ą║ą│. ą×ą┤ąĮą░ ąĖąĘ čüą╗ąŠąČąĮąŠčüč鹥ą╣ ą┐čĆąĖ čüąŠąĘą┤ą░ąĮąĖąĖ ą╝ą░ą╗ąĄąĮčīą║ąŠą╣ čĆą░ą║ąĄčéčŗ ŌĆō ą▒čÄą┤ąČąĄčéąĮą░čÅ čüąĖčüč鹥ą╝ą░ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ. ąóą░ą║čāčÄ čüąĖčüč鹥ą╝čā ą╝ąŠąČąĮąŠ ą┐ąŠčüčéčĆąŠąĖčéčī ąĮą░ ąŠčüąĮąŠą▓ąĄ MEMS-ą│ąĖčĆąŠčüą║ąŠą┐ąŠą▓. ąÆ čüčéą░čéčīąĄ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮčŗ ąĖčüč鹊čćąĮąĖą║ąĖ čüąĖčüč鹥ą╝ą░čéąĖč湥čüą║ąĖčģ ąĖ čüą╗čāčćą░ą╣ąĮčŗčģ ąŠčłąĖą▒ąŠą║ MEMS-ą│ąĖčĆąŠčüą║ąŠą┐ąŠą▓ ą┐ąŠą▓čŗčłąĄąĮąĮąŠą╣ č鹊čćąĮąŠčüčéąĖ, čüą╝ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░ąĮąŠ ą┐ąŠą▓ąĄą┤ąĄąĮąĖąĄ ą┤ą░čéčćąĖą║ą░ ą┐čĆąĖ ą▓čŗą▓ąĄą┤ąĄąĮąĖąĖ ąĮą░ ąŠčĆą▒ąĖčéčā, čüąŠą▒čĆą░ąĮą░ ą╝ąŠą┤ąĄą╗čīąĮą░čÅ čüčéą░čéąĖčüčéąĖą║ą░ č鹊čćąĮąŠčüčéąĖ ą▓čŗą▓ąĄą┤ąĄąĮąĖčÅ ąĮą░ ąŠčĆą▒ąĖčéčā čü čéą░ą║ąĖą╝ ą┤ą░čéčćąĖą║ąŠą╝.
Recently several new worldwide satellite internet projects (American one of Google and SpaceX, British OneWeb and Russian Yaliny) have been started. Each project is based on network of dozens of small satellites.In order to run smoothly broken satellites must be promptly replaced with new ones. Replacing small satellites one by one by dedicated traditional large space launch vehicles will be absurdly expensive. Launching as secondary payload is a low priced option, but preparing the primary payload often leads to huge delays. That is why a lot of start-ups in the world are trying to develop ultralight rocket that could quickly launch into space a satellites weighing from about 1 to 200 kg. One of the difficulties of creating such rocket is to design and build cheap guidance system. Really cheap rocket control system could be based on MEMS-gyroscopes.
This article is dedicated to the MEMS sensor errors, both systema- tic and stochastic, sensor behavior during simulated rocket launch and orbital insertion scattering using this sensor.

ąĪąŠąĘą┤ą░ąĮąĖąĄ čüą▓ąĄčĆčģą╗ąĄą│ą║ąĖčģ čĆą░ą║ąĄčé-ąĮąŠčüąĖč鹥ą╗ąĄą╣ (čü ą╝ą░čüčüąŠą╣ ą┐ąŠą╗ąĄąĘąĮąŠą╣ ąĮą░ą│čĆčāąĘą║ąĖ, ą▓čŗą▓ąŠą┤ąĖą╝ąŠą╣ ąĮą░ ąĮąĖąĘą║čāčÄ ąŠą║ąŠą╗ąŠąĘąĄą╝ąĮčāčÄ ąŠčĆą▒ąĖčéčā, ą┐čĆąĖą╝ąĄčĆąĮąŠ ą┤ąŠ 100 ą║ą│) ą▓ ą┐ąŠčüą╗ąĄą┤ąĮąĖąĄ ą│ąŠą┤čŗ čüčéą░ą╗ąŠ ą░ą║čéčāą░ą╗čīąĮąŠą╣ ąĘą░ą┤ą░č湥ą╣. ąŁč鹊 ą▓čŗąĘą▓ą░ąĮąŠ ą▒čāą╝ąŠą╝ ą╝ą░ą╗čŗčģ čüą┐čāčéąĮąĖą║ąŠą▓. ą£ąĮąŠąČąĄčüčéą▓ąŠ čüčéą░čĆčéą░ą┐ąŠą▓ ą▓ ą╝ąĖčĆąĄ ą┐čŗčéą░čÄčéčüčÅ čĆą░ąĘčĆą░ą▒ąŠčéą░čéčī čüą▓ąĄčĆčģą╗ąĄą│ą║čāčÄ čĆą░ą║ąĄčéčā. ąØąĖąČąĄ ą▓ čéą░ą▒ą╗ąĖčåąĄ ą┐čĆąĖą▓ąŠą┤čÅčéčüčÅ ąŠčüąĮąŠą▓ąĮčŗąĄ č鹥čģąĮąĖą║ąŠ-菹║ąŠąĮąŠą╝ąĖč湥čüą║ąĖąĄ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąĖ čéą░ą║ąĖčģ čĆą░ą║ąĄčé ąŠčé čüą░ą╝čŗčģ ąĖąĘą▓ąĄčüčéąĮčŗčģ ą║ąŠą╝ą┐ą░ąĮąĖą╣ (ą▓čüąĄą│ąŠ ąŠ ą┐ą╗ą░ąĮą░čģ čĆą░ąĘčĆą░ą▒ąŠčéą║ąĖ čüą▓ąĄčĆčģą╗ąĄą│ą║ąĖčģ čĆą░ą║ąĄčé ąĘą░čÅą▓ą╗čÅą╗ąĖ ą┤ąĄčüčÅčéą║ąĖ ąŠčĆą│ą░ąĮąĖąĘą░čåąĖą╣).
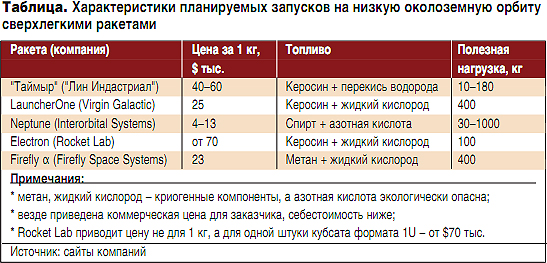
ą×ą┤ąĮą░ ąĖąĘ čüą╗ąŠąČąĮąŠčüč鹥ą╣ ą┐čĆąĖ čüąŠąĘą┤ą░ąĮąĖąĖ ą╝ą░ą╗ąĄąĮčīą║ąŠą╣ čĆą░ą║ąĄčéčŗ ŌĆō ą▒čÄą┤ąČąĄčéąĮą░čÅ čüąĖčüč鹥ą╝ą░ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ.
ąĪąŠąĘą┤ą░ąĮąĖąĄ čüąĖčüč鹥ą╝čŗ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ą┤ą╗čÅ čĆą░ą║ąĄčéčŗ-ąĮąŠčüąĖč鹥ą╗čÅ čĆą░ąĘą╝ąĄčĆąĮąŠčüčéąĖ ąĮą░ąĮąŠą║ą╗ą░čüčüą░ (ą▓ąĄą╗ąĖčćąĖąĮą░ ą┐ąŠą╗ąĄąĘąĮąŠą╣ ąĮą░ą│čĆčāąĘą║ąĖ (ą¤ąØ) ąŠčé 1 ą┤ąŠ 10, ą▓ąŠąĘą╝ąŠąČąĮąŠ, ą┤ąŠ 100 ą║ą│) ą┐ąŠą┤čĆą░ąĘčāą╝ąĄą▓ą░ąĄčé ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠčüčéčī ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÅ čüąŠą▓čĆąĄą╝ąĄąĮąĮčŗčģ 菹╗ąĄą║čéčĆąŠąĮąĮčŗčģ ą║ąŠą╝ą┐ąŠąĮąĄąĮč鹊ą▓ ą╝ą░ą╗ąŠą╣ ą╝ą░čüčüčŗ ąĖ čüč鹊ąĖą╝ąŠčüčéąĖ ą┐čĆąĖ ąŠą▒ąĄčüą┐ąĄč湥ąĮąĖąĖ ąĘą░ą┤ą░ąĮąĮčŗčģ č鹊čćąĮąŠčüčéąĖ ąĖ ąĮą░ą┤ąĄąČąĮąŠčüčéąĖ. ą×č湥ą▓ąĖą┤ąĮąŠ, čćč鹊 čŹčéąĖ čāčüą╗ąŠą▓ąĖčÅ ą┐čĆąŠčéąĖą▓ąŠčĆąĄčćą░čé ą┤čĆčāą│ ą┤čĆčāą│čā, ą┐ąŠčŹč鹊ą╝čā ą┐ąŠąĖčüą║ ąŠą┐čéąĖą╝ą░ą╗čīąĮąŠą│ąŠ čĆąĄčłąĄąĮąĖčÅ ąĘą░čéčĆčāą┤ąĮčÅąĄčéčüčÅ.
ąśčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ MEMS-č鹥čģąĮąŠą╗ąŠą│ąĖą╣ ą▓ą╝ąĄčüč鹊 ą╝ąĄčģą░ąĮąĖč湥čüą║ąĖčģ ą│ąĖčĆąŠčüą║ąŠą┐ąŠą▓ ąĖ ą░ą║čüąĄą╗ąĄčĆąŠą╝ąĄčéčĆąŠą▓ ąĖą╗ąĖ ą▓ąŠą╗ąŠą║ąŠąĮąĮąŠ-ąŠą┐čéąĖč湥čüą║ąĖčģ ą╗ą░ąĘąĄčĆąĮčŗčģ ą┤ą░čéčćąĖą║ąŠą▓ čāą│ą╗ąŠą▓ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ čéčĆąĄą▒čāąĄčé čüą┐ąĄčåąĖą░ą╗čīąĮąŠą│ąŠ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖčÅ ą▓ą▓ąĖą┤čā ą▒ąŠą╗ąĄąĄ čüąĖą╗čīąĮąŠą│ąŠ ą▓ą╗ąĖčÅąĮąĖčÅ ąĮą░ ąĮąŠą▓čŗąĄ ą┤ą░čéčćąĖą║ąĖ čäą░ą║č鹊čĆąŠą▓ čĆą░ą║ąĄčéąĮąŠą│ąŠ ą┐ąŠą╗ąĄčéą░. ąÆ ąŠčéą╗ąĖčćąĖąĄ ąŠčé ą║ąŠčüą╝ąĖč湥čüą║ąŠą│ąŠ ą░ą┐ą┐ą░čĆą░čéą░ čĆą░ą║ąĄčéą░-ąĮąŠčüąĖč鹥ą╗čī ą┐ąŠą┤ą▓ąĄčĆą│ą░ąĄčéčüčÅ ą▓ąŠąĘą┤ąĄą╣čüčéą▓ąĖčÄ čüą┐ąĄčåąĖčäąĖč湥čüą║ąĖčģ čäą░ą║č鹊čĆąŠą▓ ą║ąŠčüą╝ąĖč湥čüą║ąŠą│ąŠ ą┐ąŠą╗ąĄčéą░ ąĄą┤ąĖąĮąĖčåčŗ ą╝ąĖąĮčāčé. ąÆąĄčüčī čāčćą░čüč鹊ą║ ą▓čŗą▓ąĄą┤ąĄąĮąĖčÅ ąĮą░ ąĮąĖąĘą║čāčÄ ąŠą║ąŠą╗ąŠąĘąĄą╝ąĮčāčÄ ąŠčĆą▒ąĖčéčā ąĘą░ąĮąĖą╝ą░ąĄčé 5ŌĆō15 ą╝ąĖąĮčāčé, ą┐čĆąĖč湥ą╝ ą┤ąŠ č鹊ą│ąŠ, ą║ą░ą║ čĆą░ą║ąĄčéą░ ą┐ąŠą┤ąĮąĖą╝ąĄčéčüčÅ ą▓čŗčłąĄ 40 ą║ą╝, čāčüą╗ąŠą▓ąĖčÅ čĆą░ą▒ąŠčéčŗ čüąĖčüč鹥ą╝čŗ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ą╝ą░ą╗ąŠ ąŠčéą╗ąĖčćą░čÄčéčüčÅ ąŠčé čĆą░ą▒ąŠčéčŗ ąĮą░ ą╗čÄą▒ąŠą╝ čéčĆą░ąĮčüą┐ąŠčĆčéąĮąŠą╝ čüčĆąĄą┤čüčéą▓ąĄ.
ąĪąŠą┤ąĄčƹȹ░č鹥ą╗čīąĮąŠą╣ čćą░čüčéčīčÄ čŹč鹊ą╣ čĆą░ą▒ąŠčéčŗ čÅą▓ą╗čÅąĄčéčüčÅ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖąĄ čĆąĄą░ą╗čīąĮąŠ ą┤ąŠčüčéąĖąČąĖą╝ąŠą╣ č鹊čćąĮąŠčüčéąĖ ą▓čŗą▓ąĄą┤ąĄąĮąĖčÅ ąĮą░ ąŠčĆą▒ąĖčéčā ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ MEMS-ą┤ą░čéčćąĖą║ąŠą▓ ą┐ąŠą▓čŗčłąĄąĮąĮąŠą│ąŠ ą║ą╗ą░čüčüą░ č鹊čćąĮąŠčüčéąĖ. ą£ą░č鹥ą╝ą░čéąĖč湥čüą║ąŠąĄ ą╝ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░ąĮąĖąĄ ą┐ąŠąĘą▓ąŠą╗ąĖą╗ąŠ ąŠą┐čĆąĄą┤ąĄą╗ąĖčéčī čĆą░ąĘą▒čĆąŠčü ą┐ą░čĆą░ą╝ąĄčéčĆąŠą▓ ąŠčĆą▒ąĖčéčŗ ą▓čŗą▓ąĄą┤ąĄąĮąĖčÅ ą┐ąŠ čĆąĄą░ą╗čīąĮčŗą╝ ą┤ą░ąĮąĮčŗą╝, čüąŠą▒čĆą░ąĮąĮčŗą╝ ąĮą░ 菹║čüą┐ąĄčĆąĖą╝ąĄąĮčéą░ą╗čīąĮąŠą╣ čāčüčéą░ąĮąŠą▓ą║ąĄ (ą╝ą░ą║ąĄč鹥).
ą¤čĆąŠą▓ąĄą┤ąĄąĮąĮąŠąĄ ąĖčüčüą╗ąĄą┤ąŠą▓ą░ąĮąĖąĄ ą▓ą║ą╗čÄčćą░ąĄčé ą▓ čüąĄą▒čÅ čüąŠąĘą┤ą░ąĮąĖąĄ 菹║čüą┐ąĄčĆąĖą╝ąĄąĮčéą░ą╗čīąĮąŠą╣ čāčüčéą░ąĮąŠą▓ą║ąĖ (ą┤ą░ą╗ąĄąĄ ŌĆō ą╝ą░ą║ąĄčéą░), ą▓ą║ą╗čÄčćą░čÅ ą┐čĆąŠą│čĆą░ą╝ą╝ąĮąŠąĄ ąŠą▒ąĄčüą┐ąĄč湥ąĮąĖąĄ; ąĮą░ą▒ąŠčĆ čüčéą░čéąĖčüčéąĖą║ąĖ, ą░ąĮą░ą╗ąĖąĘ ą▓ąĄą╗ąĖčćąĖąĮ ąĖ ą┐čĆąĖčćąĖąĮ ąŠčłąĖą▒ąŠą║ ąĖ ą░ą╗ą│ąŠčĆąĖčéą╝ąŠą▓ ą┤ą╗čÅ ąĖčģ ą║ąŠčĆčĆąĄą║čåąĖąĖ.
MEMS-ą│ąĖčĆąŠčüą║ąŠą┐čŗ čüąĄą╣čćą░čü ą┐čĆąĖą╝ąĄąĮčÅčÄčéčüčÅ ąŠč湥ąĮčī čłąĖčĆąŠą║ąŠ ą▓ą▓ąĖą┤čā ąĖčģ ąĮąĖąĘą║ąŠą╣ čüč鹊ąĖą╝ąŠčüčéąĖ, ąŠą┤ąĮą░ą║ąŠ ą┤ą░čéčćąĖą║ąĖ ąĮąĖąĘčłąĄą╣ čåąĄąĮąŠą▓ąŠą╣ ą║ą░č鹥ą│ąŠčĆąĖąĖ ąĮąĄą┤ąŠčüčéą░č鹊čćąĮąŠ č鹊čćąĮčŗ ą┤ą╗čÅ ą▒ąŠą╗čīčłąĖąĮčüčéą▓ą░ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖą╣ ą▓ čüąĖčüč鹥ą╝ą░čģ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ.
MEMS-ą│ąĖčĆąŠčüą║ąŠą┐čŗ čü čåąĄąĮąŠą╣ ą┐ąŠčĆčÅą┤ą║ą░ $100 ąĘą░ ąŠčüčī ąĖą╝ąĄčÄčé ą│ąŠčĆą░ąĘą┤ąŠ ą╗čāčćčłąĖąĄ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ąĖ č鹊čćąĮąŠčüčéąĖ ąĖ čüčéą░ą▒ąĖą╗čīąĮąŠčüčéąĖ, čćč鹊 ą┐ąŠąĘą▓ąŠą╗čÅąĄčé, ą┐ąŠ ą║čĆą░ą╣ąĮąĄą╣ ą╝ąĄčĆąĄ, ą┐ąŠą┐čŗčéą░čéčīčüčÅ ą┐ąŠčüčéčĆąŠąĖčéčī ąĮą░ ąĮąĖčģ čüąĖčüč鹥ą╝čā čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ (ąĪąŻ) ą║ąŠčüą╝ąĖč湥čüą║ąŠą╣ čĆą░ą║ąĄčéčŗ.
ąźąŠčéčÅ ą▓ ą║ąŠčüą╝ąĖč湥čüą║ąŠą╣ č鹥čģąĮąĖą║ąĄ ą┐čĆąĄą┤ą╗ą░ą│ą░ą╗ąŠčüčī ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī čéą░ą║ąĖąĄ ą│ąĖčĆąŠčüą║ąŠą┐čŗ ą┤ą╗čÅ ą▒čŗčüčéčĆąŠą│ąŠ ą▓ąŠčüčüčéą░ąĮąŠą▓ą╗ąĄąĮąĖčÅ ąŠčĆąĖąĄąĮčéą░čåąĖąĖ ą┐ąŠ ąĘą▓ąĄąĘą┤ąĮąŠą╝čā ą┤ą░čéčćąĖą║čā [1], ąĮąĖą║č鹊 ąĮąĄ čüčéą░ą▓ąĖą╗ čåąĄą╗čīčÄ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī ąĖčģ ą║ą░ą║ ą┐ąĄčĆą▓ąĖčćąĮčŗąĄ ą┤ą░čéčćąĖą║ąĖ ąŠčĆąĖąĄąĮčéą░čåąĖąĖ.
ąĪčéčĆąŠą│ąŠ ą│ąŠą▓ąŠčĆčÅ, ą┐ąŠą╗ąĮąŠčüčéčīčÄ čéą▓ąĄčĆą┤ąŠč鹊ą┐ą╗ąĖą▓ąĮą░čÅ čĆą░ą║ąĄčéą░ čü ąĮą░ą║ą╗ąŠąĮąĮčŗą╝ čüčéą░čĆč鹊ą╝, ą║ą░ą║ čĆą░ąĮąĮąĖąĄ čÅą┐ąŠąĮčüą║ąĖąĄ čĆą░ą║ąĄčéčŗ-ąĮąŠčüąĖč鹥ą╗ąĖ Lamb-da-4S [2] ąĖ Mu-4S [3], ą╝ąŠąČąĄčé ą▓čŗą▓ąĄčüčéąĖ ąĮą░ ąŠčĆą▒ąĖčéčā čüą┐čāčéąĮąĖą║, ą▓ąŠąŠą▒čēąĄ ąĮąĄ ąĖčüą┐ąŠą╗čīąĘčāčÅ ąĖąĮąĄčĆčåąĖą░ą╗čīąĮčāčÄ ąĪąŻ ąĖą╗ąĖ čĆą░ą┤ąĖąŠč鹥čģąĮąĖč湥čüą║ąŠąĄ ą┤ąĖčüčéą░ąĮčåąĖąŠąĮąĮąŠąĄ čāą┐čĆą░ą▓ą╗ąĄąĮąĖąĄ. ąÆ Lambda-4S ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ą╗ą░čüčī ąŠą┤ąĮąŠąŠčüąĮą░čÅ ąŠčĆąĖąĄąĮčéą░čåąĖčÅ, ąĄąĄ ą┤ą░čéčćąĖą║ąŠą╝ čüą╗čāąČąĖą╗ č湥čéčŗčĆąĄčģčĆą░ą╝ąŠčćąĮčŗą╣ ą╝ąĄčģą░ąĮąĖč湥čüą║ąĖą╣ ą│ąĖčĆąŠčüą║ąŠą┐. ąÆą╝ąĄčüč鹊 čŹč鹊ą│ąŠ ą╝ąŠąČąĮąŠ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī ąŠą┤ąĮąŠąŠčüąĮčāčÄ čüąŠą╗ąĮąĄčćąĮčāčÄ ąŠčĆąĖąĄąĮčéą░čåąĖčÄ. ąĢčüą╗ąĖ ą┐čĆą░ą▓ąĖą╗čīąĮąŠ ą▓čŗą▒čĆą░čéčī ą╝ąŠą╝ąĄąĮčé ąĘą░ą┐čāčüą║ą░, čćč鹊ą▒čŗ ąĮą░ą┐čĆą░ą▓ą╗ąĄąĮąĖąĄ ąĮą░ čåąĄąĮčéčĆ ąĪąŠą╗ąĮčåą░ čüąŠą▓ą┐ą░ą┤ą░ą╗ąŠ čü ąČąĄą╗ą░ąĄą╝čŗą╝ ą┐ąŠą╗ąŠąČąĄąĮąĖąĄą╝ ąŠčüąĖ čĆą░ą║ąĄčéčŗ, ą╝ąŠąČąĮąŠ čüąŠčĆąĖąĄąĮčéąĖčĆąŠą▓ą░čéčī čĆą░ą║ąĄčéčā ą┐ąŠ čüąŠą╗ąĮąĄčćąĮąŠą╝čā ą┤ą░čéčćąĖą║čā ąĖ, ą┐ąŠ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĮąŠą╝čā ąĘą░ą║ąŠąĮčā čĆą░čüčüčćąĖčéą░ą▓ ą▓ąĄčĆčłąĖąĮčā čéčĆą░ąĄą║č鹊čĆąĖąĖ, ąĘą░ą┐čāčüčéąĖčéčī ąĀąöąóąó, č鹊 čüą┐čāčéąĮąĖą║ ą▓čŗą╣ą┤ąĄčé ąĮą░ ąŠčĆą▒ąĖčéčā.
ą×ą┤ąĮą░ą║ąŠ ąĮą░čćąĖąĮą░čÅ čü ąĮąĄą║ąŠč鹊čĆąŠą╣ čĆą░ąĘą╝ąĄčĆąĮąŠčüčéąĖ, ąČąĖą┤ą║ąŠčüčéąĮčŗąĄ čüčéčāą┐ąĄąĮąĖ ąŠą║ą░ąĘčŗą▓ą░čÄčéčüčÅ ą┤ąĄčłąĄą▓ą╗ąĄ čéą▓ąĄčĆą┤ąŠč鹊ą┐ą╗ąĖą▓ąĮčŗčģ, ą┐ąŠčŹč鹊ą╝čā 菹║ąŠąĮąŠą╝ąĖč湥čüą║ąĖ čåąĄą╗ąĄčüąŠąŠą▒čĆą░ąĘąĮąŠ ą┐ąŠą┐čŗčéą░čéčīčüčÅ ą┐ąŠčüčéčĆąŠąĖčéčī čéą░ą║čāčÄ čĆą░ą║ąĄčéčā, ąĖčüą┐ąŠą╗čīąĘčāčÅ ą¢ąĀąö ąĮą░ ą┐ąĄčĆą▓ąŠą╣ čüčéčāą┐ąĄąĮąĖ. ąØąŠ ąČąĖą┤ą║ąŠčüčéąĮą░čÅ čüčéčāą┐ąĄąĮčī čéčĆąĄą▒čāąĄčé ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą│ąŠ čüčéą░čĆčéą░ ąĖ ąŠą│čĆą░ąĮąĖč湥ąĮąĖčÅ čāą│ą╗ą░ ą░čéą░ą║ąĖ ąĖąĘ-ąĘą░ ą╝ą░ą╗ąŠą│ąŠ ąĘą░ą┐ą░čüą░ ą┐čĆąŠčćąĮąŠčüčéąĖ ą║ąŠąĮčüčéčĆčāą║čåąĖąĖ ąĖ ą╝ąĄąĮčīčłąĄą╣ čéčÅą│ąŠą▓ąŠąŠčĆčāąČąĄąĮąĮąŠčüčéąĖ. ąĪą╗ąĄą┤ąŠą▓ą░č鹥ą╗čīąĮąŠ, čéą░ą║ąŠą╣ čĆą░ą║ąĄč鹥 ą┐ąŠąĮą░ą┤ąŠą▒ąĖčéčüčÅ ą┤ąĄčłąĄą▓ą░čÅ ąĖ ą╝ą░ą╗ąŠą│ą░ą▒ą░čĆąĖčéąĮą░čÅ čüąĖčüč鹥ą╝ą░ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ. ąĪ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄą╝ MEMS-ą┤ą░čéčćąĖą║ąŠą▓ ą╝ąŠąČąĮąŠ čüąŠąĘą┤ą░čéčī ąĪąŻ ą╝ą░čüčüąŠą╣ ą╝ąĄąĮąĄąĄ 1 ą║ą│ (ąĮąĄ čüčćąĖčéą░čÅ ą║ą░ą▒ąĄą╗čīąĮąŠą╣ čüąĄčéąĖ ąĖ ąĖčüą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčŗčģ ąŠčĆą│ą░ąĮąŠą▓).
ąöą╗čÅ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĖčÅ ą┐čĆąĖą╝ąĄąĮąĖą╝ąŠčüčéąĖ MEMS-ą│ąĖčĆąŠčüą║ąŠą┐ąŠą▓ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠ čģąŠčéčÅ ą▒čŗ čćą░čüčéąĖčćąĮąŠ čüą╝ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░čéčī čāčüą╗ąŠą▓ąĖčÅ ą┐ąŠą╗ąĄčéą░ ąĮą░ čĆą░ą║ąĄč鹥 ąĖ ą▓ąŠčüą┐čĆąŠąĖąĘą▓ąĄčüčéąĖ, ąĮą░čüą║ąŠą╗čīą║ąŠ čŹč鹊 ą▓ąŠąĘą╝ąŠąČąĮąŠ, čĆąĄą░ą║čåąĖčÄ ąĖčüą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮčŗčģ ąŠčĆą│ą░ąĮąŠą▓ ąĮą░ čüąĖą│ąĮą░ą╗čŗ, ą┐ąŠčüčéčāą┐ą░čÄčēąĖąĄ čü MEMS-ą┤ą░čéčćąĖą║ąŠą▓.
ąöą╗čÅ ą┐ąŠąĖčüą║ąŠą▓čŗčģ čĆą░ą▒ąŠčé ą┐čĆąĖ ą▒ąŠą╗čīčłąŠą╣ čüč鹥ą┐ąĄąĮąĖ ąĮąĄąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĮąŠčüčéąĖ ą║ąŠąĮąĄčćąĮąŠą│ąŠ čĆąĄąĘčāą╗čīčéą░čéą░ ą▒čŗą╗ą░ ą▓čŗą▒čĆą░ąĮą░ čüčģąĄą╝ą░ čĆą░ą║ąĄčéčŗ-ąĮąŠčüąĖč鹥ą╗čÅ, ąŠą▒ąĄčēą░ą▓čłą░čÅ ą╝ąĖąĮąĖą╝ą░ą╗čīąĮčāčÄ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī ąŠčé č鹊čćąĮąŠčüčéąĖ ąĖčüą┐ąŠą╗čīąĘčāąĄą╝ąŠą│ąŠ ą│ąĖčĆąŠčüą║ąŠą┐ą░. ąØąĄą║ąŠč鹊čĆąŠąĄ "ąĮčāą╗ąĄą▓ąŠąĄ" ą┐čĆąĖą▒ą╗ąĖąČąĄąĮąĖąĄ čéčĆąĄą▒ąŠą▓ą░ą╗ąŠ čüąĮąĖąČąĄąĮąĖčÅ čéčĆąĄą▒ąŠą▓ą░ąĮąĖą╣ ą║ ą│ąĖčĆąŠčüą║ąŠą┐ą░ą╝, ą┐ąŠčŹč鹊ą╝čā ą▒čŗą╗ąŠ čĆąĄčłąĄąĮąŠ ą▓ ą╝ąŠą┤ąĄą╗ąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░čéčī ą▓ąĄčĆčģąĮąĖąĄ čüčéčāą┐ąĄąĮąĖ ąĮą░ ąĀąöąóąó, čüčéą░ą▒ąĖą╗ąĖąĘąĖčĆčāąĄą╝čŗąĄ ą▓čĆą░čēąĄąĮąĖąĄą╝.
ąĪąĖčüč鹥ą╝ą░ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ą┤ąŠą╗ąČąĮą░ čĆą░ą▒ąŠčéą░čéčī ą▓ čüąŠčüčéą░ą▓ąĄ ą│ąĖą┐ąŠč鹥čéąĖč湥čüą║ąŠą╣ čéčĆąĄčģčüčéčāą┐ąĄąĮčćą░č鹊ą╣ čĆą░ą║ąĄčéčŗ, čā ą║ąŠč鹊čĆąŠą╣ ą┐ąĄčĆą▓ą░čÅ čüčéčāą┐ąĄąĮčī ąČąĖą┤ą║ąŠčüčéąĮą░čÅ čüąŠ ą▓čĆąĄą╝ąĄąĮąĄą╝ čĆą░ą▒ąŠčéčŗ ąŠą║ąŠą╗ąŠ 150 čüąĄą║., ą░ ą▓ąĄčĆčģąĮąĖąĄ ą┤ą▓ąĄ ŌĆō čéą▓ąĄčĆą┤ąŠč鹊ą┐ą╗ąĖą▓ąĮčŗąĄ čü ąĮąĄą▒ąŠą╗čīčłąĖą╝ ą▓čĆąĄą╝ąĄąĮąĄą╝ čĆą░ą▒ąŠčéčŗ. ą¤ąŠą┤čĆą░ąĘčāą╝ąĄą▓ą░ąĄčéčüčÅ, čćč鹊 ą▓ąŠ ą▓čĆąĄą╝čÅ ą▒ą░ą╗ą╗ąĖčüčéąĖč湥čüą║ąŠą╣ ą┐ą░čāąĘčŗ ąĖ ą┐čĆąĖčåąĄą╗ąĖą▓ą░ąĮąĖčÅ ą┐ąŠ ąĪąŠą╗ąĮčåčā ąŠčĆąĖąĄąĮčéą░čåąĖčÅ ąŠą▒ąĄčüą┐ąĄčćąĖą▓ą░ąĄčéčüčÅ ą│ą░ąĘąŠą▓čŗą╝ąĖ čüąŠą┐ą╗ą░ą╝ąĖ, čĆą░ą▒ąŠčéą░čÄčēąĖą╝ąĖ ąĮą░ ą│ą░ąĘąĄ ąĮą░ą┤ą┤čāą▓ą░ 1-ą╣ čüčéčāą┐ąĄąĮąĖ.
ą£ąŠą┤ąĄą╗čīąĮą░čÅ čāčüčéą░ąĮąŠą▓ą║ą░ ą┤ąŠą╗ąČąĮą░ ąŠą▒ąĄčüą┐ąĄčćąĖčéčī ąŠčéą║ą╗ąŠąĮąĄąĮąĖąĄ ąĖąĘą╝ąĄčĆąĖč鹥ą╗čīąĮąŠą│ąŠ 菹╗ąĄą╝ąĄąĮčéą░ ą┤ą╗čÅ ąĖą╝ąĖčéą░čåąĖąĖ ą┐čĆąŠą│čĆą░ą╝ą╝čŗ ą┐ąŠą╗ąĄčéą░ ą║ą░ą║ ą╝ąĖąĮąĖą╝čāą╝ ą┐ąŠ ą┤ą▓čāą╝ čāą│ą╗ą░ą╝ ŌĆō čéą░ąĮą│ą░ąČą░ ąĖ čĆčŗčüą║ą░ąĮąĖčÅ. ąŻą┐čĆą░ą▓ą╗čÅčÄčēą░čÅ ą┐čĆąŠą│čĆą░ą╝ą╝ą░ ą┤ąŠą╗ąČąĮą░ ąŠą▒ąĄčüą┐ąĄčćąĖą▓ą░čéčī ą┐ąĄčĆąĄą┤ą░čćčā ą┤ą░ąĮąĮčŗčģ ąĮą░ ą┐ąĄčĆčüąŠąĮą░ą╗čīąĮčŗą╣ ą║ąŠą╝ą┐čīčÄč鹥čĆ ą┤ą╗čÅ čĆąĄą│ąĖčüčéčĆą░čåąĖąĖ ąĖ ą┤ą░ą╗čīąĮąĄą╣čłąĄą╣ ąŠą▒čĆą░ą▒ąŠčéą║ąĖ.
ąŻčüčéą░ąĮąŠą▓ą║ą░ čüąŠčüč鹊ąĖčé ąĖąĘ ą│ąŠą╗ąŠą▓ą║ąĖ čü ą┤ą░čéčćąĖą║ą░ą╝ąĖ, ą┤ą▓čāčģą║ąŠąŠčĆą┤ąĖąĮą░čéąĮąŠą│ąŠ ą║ą░čćą░čÄčēąĄą│ąŠčüčÅ čüč鹊ą╗ą░ čü 菹╗ąĄą║čéčĆąŠą╝ąĄčģą░ąĮąĖč湥čüą║ąĖą╝ąĖ ą┐čĆąĖą▓ąŠą┤ą░ą╝ąĖ, ą┐ą╗ą░čéčŗ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ, ąĖčüč鹊čćąĮąĖą║ą░ ą┐ąĖčéą░ąĮąĖčÅ (čüą╝. čĆąĖčü. 1). ąÜ čāčüčéą░ąĮąŠą▓ą║ąĄ ą┤ą╗čÅ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ą┐ąŠą┤ą║ą╗čÄčćą░ąĄčéčüčÅ ą┐ąĄčĆčüąŠąĮą░ą╗čīąĮčŗą╣ ą║ąŠą╝ą┐čīčÄč鹥čĆ č湥čĆąĄąĘ ą┐ąŠčüą╗ąĄą┤ąŠą▓ą░č鹥ą╗čīąĮčŗą╣ ą┐ąŠčĆčé (RS-232).

ąöą░čéčćąĖą║ ADIS16300 ą▓ą║ą╗čÄčćą░ąĄčé MEMS-ą│ąĖčĆąŠčüą║ąŠą┐ (ą┤ą░čéčćąĖą║ čāą│ą╗ąŠą▓ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ) ą┐ąŠ ąŠčüąĖ Z čü čåąĖčäčĆąŠą▓čŗą╝ ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮąĖąĄą╝ ą▓čŗčģąŠą┤ąĮąŠą╣ ąĖąĮč乊čĆą╝ą░čåąĖąĖ, 3-ąŠčüąĮčŗą╣ MEMS-ą░ą║čüąĄą╗ąĄčĆąŠą╝ąĄčéčĆ ą┐ąŠ ąŠčüčÅą╝ X, Y, Z, ą┤ą░čéčćąĖą║ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčŗ ą┤ą╗čÅ ą║ąŠčĆčĆąĄą║čåąĖąĖ ąĮčāą╗čÅ ą│ąĖčĆąŠčüą║ąŠą┐ąŠą▓ ąĖ čé.ą┤. [4].
ąØą░ čĆąĖčü. 2 ą┐čĆąĖą▓ąĄą┤ąĄąĮ ą│čĆą░čäąĖą║ ą║ą▓ą░ą┤čĆą░čéąĮąŠą│ąŠ ą║ąŠčĆąĮčÅ ąĖąĘ ą▓ą░čĆąĖą░čåąĖąĖ ąÉą╗ą╗ą░ąĮą░, ąŠą┐ąĖčüčŗą▓ą░čÄčēąĖą╣ č鹊čćąĮąŠčüčéčī ąĖ čüčéą░ą▒ąĖą╗čīąĮąŠčüčéčī ą│ąĖčĆąŠčüą║ąŠą┐ą░. ąśąĘ čŹč鹊ą│ąŠ ą│čĆą░čäąĖą║ą░ čüą╗ąĄą┤čāąĄčé, čćč鹊 čüčéą░ą▒ąĖą╗čīąĮąŠčüčéčī ą│ąĖčĆąŠčüą║ąŠą┐ą░ ąĮą░ ą▓čĆąĄą╝ąĄąĮąĮčŗčģ ąĖąĮč鹥čĆą▓ą░ą╗ą░čģ ą▒ąŠą╗ąĄąĄ 100 čüąĄą║. ąŠą┐čĆąĄą┤ąĄą╗čÅąĄčéčüčÅ čäą╗ąĖą║ąĄčĆ-čłčāą╝ąŠą╝ ąĖ ąĮąĄ ą╝ąŠąČąĄčé ąŠą▒ąĄčüą┐ąĄčćąĖčéčī ą▓ąĄą╗ąĖčćąĖąĮčā ą┤čĆąĄą╣čäą░ ą╗čāčćčłąĄ 25 ą│čĆą░ą┤. ą▓ čćą░čü. ą¤ąŠą╝ąĖą╝ąŠ čŹč鹊ą│ąŠ ąĮą░ čüčéą░ą▒ąĖą╗čīąĮąŠčüčéčī ąĮčāą╗čÅ ą│ąĖčĆąŠčüą║ąŠą┐ą░ ą▓ą╗ąĖčÅąĄčé č鹥ą╝ą┐ąĄčĆą░čéčāčĆą░ ą┤ą░čéčćąĖą║ą░, ą║ąŠč鹊čĆčāčÄ čéčĆąĄą▒čāąĄčéčüčÅ ą║ąŠąĮčéčĆąŠą╗ąĖčĆąŠą▓ą░čéčī. ąØą░ą║ąŠąĮąĄčå, čéčĆąĄčéčīąĖą╝ ąĖčüč鹊čćąĮąĖą║ąŠą╝ ąŠčłąĖą▒ąŠą║ čÅą▓ą╗čÅąĄčéčüčÅ ą┐ą░čĆą░ąĘąĖčéąĮą░čÅ čćčāą▓čüčéą▓ąĖč鹥ą╗čīąĮąŠčüčéčī ą║ ą╗ąĖąĮąĄą╣ąĮąŠą╝čā čāčüą║ąŠčĆąĄąĮąĖčÄ, ą║ąŠč鹊čĆą░čÅ ąĮąĄąŠą┤ąĖąĮą░ą║ąŠą▓ą░ ą┤ą╗čÅ čĆą░ąĘąĮčŗčģ ąŠčüąĄą╣.
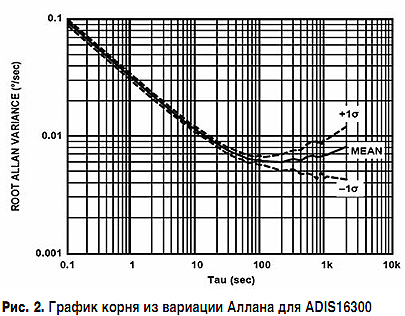
ąŚą░ ą▓čĆąĄą╝čÅ ąŠčé čüčéą░čĆčéą░ ą┤ąŠ ą║ąŠčĆčĆąĄą║čåąĖąĖ ą┐ąŠ čüąŠą╗ąĮąĄčćąĮąŠą╝čā ą┤ą░čéčćąĖą║čā (ąĮąŠą╝ąĖąĮą░ą╗čīąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ 300 čüąĄą║.) ą┐čĆąĖ čģąŠčĆąŠčłąĄą╣ ą║ąŠą╝ą┐ąĄąĮčüą░čåąĖąĖ ą┐ą░čĆą░ąĘąĖčéąĮčŗčģ čŹčäč乥ą║č鹊ą▓ čāčģąŠą┤ ą╝ąŠąČąĄčé čüąŠčüčéą░ą▓ąĖčéčī ąŠą║ąŠą╗ąŠ 2 ą│čĆą░ą┤.
ąöą░čéčćąĖą║ ADIS16251, čüč鹊čÅčēąĖą╣ ą▓ ą║ą░ąĮą░ą╗ąĄ čĆčŗčüą║ą░ąĮąĖčÅ, ąŠą▒ą╗ą░ą┤ą░ąĄčé ą┐ąŠčģąŠąČąĖą╝ ąĮą░ą▒ąŠčĆąŠą╝ čüą▓ąŠą╣čüčéą▓, ąĮąŠ ąŠčéąĮąŠčüąĖčéčüčÅ ą║ ą┐čĆąĄą┤čŗą┤čāčēąĄą╝čā ą┐ąŠą║ąŠą╗ąĄąĮąĖčÄ, ąĖąĘ-ąĘą░ č湥ą│ąŠ ąĄą│ąŠ ąĘą░čÅą▓ą╗ąĄąĮąĮą░čÅ čüčéą░ą▒ąĖą╗čīąĮąŠčüčéčī ą┐čĆąĖą╝ąĄčĆąĮąŠ ą▓ą┤ą▓ąŠąĄ čģčāąČąĄ.
ąŻą┐čĆą░ą▓ą╗čÅčÄčēą░čÅ ą┐čĆąŠą│čĆą░ą╝ą╝ą░ ą▒čŗą╗ą░ ąĮą░ą┐ąĖčüą░ąĮą░ ąĮą░ ą░čüčüąĄą╝ą▒ą╗ąĄčĆąĄ AVR8, ą░ ą▓čŗą┐ąŠą╗ąĮčÅčéčī čüą╗ąŠąČąĮčŗąĄ ą╝ą░č鹥ą╝ą░čéąĖč湥čüą║ąĖąĄ ą▓čŗčćąĖčüą╗ąĄąĮąĖčÅ ąĮą░ ą░čüčüąĄą╝ą▒ą╗ąĄčĆąĄ ąĮąĄčāą┤ąŠą▒ąĮąŠ. ą¤ąŠčŹč鹊ą╝čā ą┤ą╗čÅ ą▓ąĮčāčéčĆąĄąĮąĮąĖčģ ą▓čŗčćąĖčüą╗ąĄąĮąĖą╣ ąĖčüą┐ąŠą╗čīąĘčāčÄčéčüčÅ čāą┐čĆąŠčēąĄąĮąĮčŗąĄ č乊čĆą╝čāą╗čŗ ąĖ ą░ą╗ą│ąŠčĆąĖčéą╝čŗ. ąÆ čüą╗čāčćą░ąĄ čćąĖčüą╗ąĄąĮąĮąŠą│ąŠ ąĖąĮč鹥ą│čĆąĖčĆąŠą▓ą░ąĮąĖčÅ čŹč鹊 ą┐čĆąĖą▓ąŠą┤ąĖčé ą║ ą┐ąŠč鹥čĆąĄ č鹊čćąĮąŠčüčéąĖ, ąŠą┤ąĮą░ą║ąŠ č鹊čćąĮąŠčüčéčī čüą░ą╝ąŠą│ąŠ ą┤ą░čéčćąĖą║ą░ ą╗ąĖą╝ąĖčéąĖčĆčāąĄčé č鹊čćąĮąŠčüčéčī ą┐ąŠą╗čāčćą░ąĄą╝čŗčģ čĆąĄąĘčāą╗čīčéą░č鹊ą▓ ą┤ą░ąČąĄ čüąĖą╗čīąĮąĄąĄ. ą¤ąŠčŹč鹊ą╝čā čćąĖčüą╗ąĄąĮąĮąŠąĄ ąĖąĮč鹥ą│čĆąĖčĆąŠą▓ą░ąĮąĖąĄ čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮąŠ ą▓ ą┐čĆąŠčüč鹥ą╣čłąĄą╝ ą▓ąĖą┤ąĄ, ą╝ąĄč鹊ą┤ąŠą╝ ą┐čĆčÅą╝ąŠčāą│ąŠą╗čīąĮąĖą║ąŠą▓ [5], čćč鹊 ą┐ąŠąĘą▓ąŠą╗čÅąĄčé ąŠą▒ąŠą╣čéąĖčüčī ą▒ąĄąĘ čāą╝ąĮąŠąČąĄąĮąĖčÅ ą▒ą╗ą░ą│ąŠą┤ą░čĆčÅ čāą┤ą░čćąĮąŠ ą▓čŗą▒čĆą░ąĮąĮąŠą╝čā ą▓ąĄčüčā ą╝ą╗ą░ą┤čłąĄą│ąŠ čĆą░ąĘčĆčÅą┤ą░ ąĖ ą▓čĆąĄą╝ąĄąĮąĮąŠą│ąŠ ą║ą▓ą░ąĮčéą░. ą¦ą░čüč鹊čéą░ ąŠą▒ąĮąŠą▓ą╗ąĄąĮąĖčÅ ADIS16300 čĆą░ą▓ąĮą░ 819,2 ąōčå, ą▓ąĄčü ąĄą┤ąĖąĮąĖčåčŗ ą╝ą╗ą░ą┤čłąĄą│ąŠ čĆą░ąĘčĆčÅą┤ą░ čüąŠčüčéą░ą▓ą╗čÅąĄčé 1/80 ą│čĆą░ą┤. čāą│ą╗ą░ ą▓ čüąĄą║.: 1/819,2*1/80=1/65536.
ą¤čĆąĖ čéą░ą║ąĖčģ čćą░čüč鹊č鹥 ąŠą▒ąĮąŠą▓ą╗ąĄąĮąĖčÅ ąĖ ą▓ąĄčüąĄ ą╝ą╗ą░ą┤čłąĄą│ąŠ čĆą░ąĘčĆčÅą┤ą░ ą╝ąĄč鹊ą┤ ą┐čĆčÅą╝ąŠčāą│ąŠą╗čīąĮąĖą║ąŠą▓ ą┤ą░ąĄčé ą┤ąŠčüčéą░č鹊čćąĮčāčÄ č鹊čćąĮąŠčüčéčī. ąøąĄą│ą║ąŠ ąŠą┐čĆąĄą┤ąĄą╗ąĖčéčī, čćč鹊 ąĮą░ čĆą░ąĘą▓ąŠčĆąŠč鹥 ąŠčé 90 ą┤ąŠ 0 ą│čĆą░ą┤. ąĘą░ 180 čüąĄą║. ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮą░čÅ ąŠčłąĖą▒ą║ą░ ąĮąĄ ą┐čĆąĄą▓čŗčüąĖčé 1,125 ą│čĆą░ą┤.
ąöą╗čÅ ą┐čĆąĄą┤ą▓ą░čĆąĖč鹥ą╗čīąĮąŠą│ąŠ ą░ąĮą░ą╗ąĖąĘą░ č鹊čćąĮąŠčüčéąĖ MEMS-ą┤ą░čéčćąĖą║ąŠą▓ čåąĄą╗ąĄčüąŠąŠą▒čĆą░ąĘąĮąŠ ą┐čĆąĖą╝ąĄąĮąĖčéčī ą┐čĆąŠčüč鹥ą╣čłčāčÄ ą╝ąŠą┤ąĄą╗čī, ą║ąŠč鹊čĆą░čÅ ąĮąĄ ą▒čāą┤ąĄčé ą▓ą║ą╗čÄčćą░čéčī čāą│ąŠą╗ ą║čĆąĄąĮą░, ą░ č鹊ą╗čīą║ąŠ čāą│ą╗čŗ čĆčŗčüą║ą░ąĮąĖčÅ ąĖ čéą░ąĮą│ą░ąČą░. ąŻč湥čé ąŠčłąĖą▒ą║ąĖ, ą▓ąĮąŠčüąĖą╝čŗą╣ ą┤čĆąĄą╣č乊ą╝ ą┐ąŠ ą║čĆąĄąĮčā, ą┤ąŠą▓ąŠą╗čīąĮąŠ čüą╗ąŠąČąĄąĮ ąĖ ąĮą░ ą┤ą░ąĮąĮąŠą╝ čŹčéą░ą┐ąĄ ąĮąĄčåąĄą╗ąĄčüąŠąŠą▒čĆą░ąĘąĄąĮ.
ą¤ąŠ ą░ąĮą░ą╗ąŠą│ąĖčćąĮčŗą╝ ą┐čĆąĖčćąĖąĮą░ą╝ ą┐čĆąĖčłą╗ąŠčüčī ąŠčéą║ą░ąĘą░čéčīčüčÅ ąĖ ąŠčé ą╝ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ č鹥čĆą╝ąĖąĮą░ą╗čīąĮąŠą│ąŠ ąĮą░ą▓ąĄą┤ąĄąĮąĖčÅ, ą▒ąŠą╗ąĄąĄ čåąĄą╗ąĄčüąŠąŠą▒čĆą░ąĘąĮčŗą╝ ą┤ą╗čÅ "ąĮčāą╗ąĄą▓ąŠą│ąŠ" ą┐čĆąĖą▒ą╗ąĖąČąĄąĮąĖčÅ ą▓čŗą│ą╗čÅą┤ąĖčé ąČąĄčüčéą║ąĖą╣ ąĘą░ą║ąŠąĮ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ. ą¤ąŠčüą║ąŠą╗čīą║čā ą▓ąĄčĆčģąĮąĖąĄ čüčéčāą┐ąĄąĮąĖ ą╝ąŠą┤ąĄą╗ąĖčĆčāąĄą╝ąŠą╣ čĆą░ą║ąĄčéčŗ ąĖčüą┐ąŠą╗čīąĘčāčÄčé ąĀąöąóąó, ą┐čĆąĖčłą╗ąŠčüčī ąŠčéą║ą░ąĘą░čéčīčüčÅ ąĖ ąŠčé čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ą║ą░ąČčāčēąĄą╣čüčÅ čüą║ąŠčĆąŠčüčéčīčÄ.
ąØą░ ąĖčüč鹊čĆąĖč湥čüą║ąĖčģ ą┐čĆąĖą╝ąĄčĆą░čģ [6] ąĖąĘą▓ąĄčüčéąĮąŠ, čćč鹊 ą┐ąĄčĆą▓čŗąĄ čāą┐čĆą░ą▓ą╗čÅąĄą╝čŗąĄ ą▒ą░ą╗ą╗ąĖčüčéąĖč湥čüą║ąĖąĄ čĆą░ą║ąĄčéčŗ ąĮąĄ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ą╗ąĖ čüąĖčüč鹥ą╝čā čüčéą░ą▒ąĖą╗ąĖąĘą░čåąĖąĖ čåąĄąĮčéčĆą░ ą╝ą░čüčü ąĖ čüąĖčüč鹥ą╝čā ąŠą┤ąĮąŠą▓čĆąĄą╝ąĄąĮąĮąŠą│ąŠ ąŠą┐ąŠčĆąŠąČąĮąĄąĮąĖčÅ ą▒ą░ą║ąŠą▓. ąŁč鹊 ą┐čĆąĖą▓ąŠą┤ąĖčé ą║ ą┐ąŠč鹥čĆčÅą╝ ą▓ ą┤ą░ą╗čīąĮąŠčüčéąĖ ąĖ č鹊čćąĮąŠčüčéąĖ, ąŠą┤ąĮą░ą║ąŠ čüčĆą░ą▓ąĮąĖą╝čŗąĄ ą┐ąŠč鹥čĆąĖ ą┐čĆąĖą▓ąĮąŠčüąĖčé ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĄ ą┐čĆąŠčüč鹥ą╣čłąĄą╣ ą┐čĆąŠą│čĆą░ą╝ą╝čŗ čāą│ą╗ą░ čéą░ąĮą│ą░ąČą░.
ą¤ąŠčŹč鹊ą╝čā ąĮą░ ą┤ą░ąĮąĮąŠą╝ čŹčéą░ą┐ąĄ čåąĄą╗ąĄčüąŠąŠą▒čĆą░ąĘąĮąŠ ąŠą│čĆą░ąĮąĖčćąĖčéčīčüčÅ ą╝ąŠą┤ąĄą╗čīčÄ "ą┐ą╗ąŠčüą║ąŠą╣" ąŚąĄą╝ą╗ąĖ (čé.ąĄ. čåąĄą╗ąĄą▓ąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ čāą│ą╗ą░ čéą░ąĮą│ą░ąČą░ ą▓ ą║ąŠąĮčåąĄ čéčĆą░ąĄą║č鹊čĆąĖąĖ ą┐čĆąĖąĮąĖą╝ą░ąĄčéčüčÅ čĆą░ą▓ąĮčŗą╝ ąĮčāą╗čÄ), ąĮąĄ čāčćąĖčéčŗą▓ą░čéčī ąĮąĄčåąĄąĮčéčĆą░ą╗čīąĮąŠčüčéčī ą│čĆą░ą▓ąĖčéą░čåąĖąŠąĮąĮąŠą│ąŠ ą┐ąŠą╗čÅ. ąöą╗čÅ ą╝ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ ą▓čŗą▓ąŠą┤ą░ ąĮą░ ąŠčĆą▒ąĖčéčā ąĖčüą┐ąŠą╗čīąĘčāąĄčéčüčÅ čüą┐čĆąĄą┤čłąĖčé Launchmodel [7], ąĮą░ą┐ąĖčüą░ąĮąĮčŗą╣ ąÜąĖčĆąĖą╗ą╗ąŠą╝ ąøąĄą▓ąĖąĮčŗą╝ ą┤ą╗čÅ ą┐čĆąŠą│čĆą░ą╝ą╝čŗ Microsoft Excel, ą║ą░ą║ ą┐čĆąŠčüč鹊ą╣ ą▓ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ ąĖ ą┤ąŠčüčéą░č鹊čćąĮąŠ č鹊čćąĮčŗą╣ čĆą░čüč湥čéąĮčŗą╣ ąĖąĮčüčéčĆčāą╝ąĄąĮčé.
ą¤čĆąĖ ą┐čĆąŠą▓ąĄčĆą║ąĄ čĆą░ą▒ąŠčéčŗ ą┐čĆąŠą│čĆą░ą╝ą╝čŗ čāą│ą╗ą░ čéą░ąĮą│ą░ąČą░ ą▒čŗą╗ąŠ ąŠą▒ąĮą░čĆčāąČąĄąĮąŠ ąĘąĮą░čćąĖč鹥ą╗čīąĮąŠąĄ čüąĖčüč鹥ą╝ą░čéąĖč湥čüą║ąŠąĄ čĆą░čüčģąŠąČą┤ąĄąĮąĖąĄ ą╝ąĄąČą┤čā čāą│ą╗ąŠą╝ čéą░ąĮą│ą░ąČą░, ąĖąĘą╝ąĄčĆąĄąĮąĮčŗą╝ čü ą┐ąŠą╝ąŠčēčīčÄ ą░ą║čüąĄą╗ąĄčĆąŠą╝ąĄčéčĆą░-ąĖąĮą║ą╗ąĖąĮąŠą╝ąĄčéčĆą░, ą▓čģąŠą┤čÅčēąĄą│ąŠ ą▓ čüąŠčüčéą░ą▓ ADIS16300, ąĖ ą▓čŗčćąĖčüą╗ąĄąĮąĮąŠą│ąŠ ąĖąĮč鹥ą│čĆąĖčĆąŠą▓ą░ąĮąĖąĄą╝ ą┐ąŠ ą┤ą░ąĮąĮčŗą╝ ą│ąĖčĆąŠčüą║ąŠą┐ą░, ą┤ąŠčüčéąĖą│ą░ą▓čłąĄąĄ 20 ą│čĆą░ą┤. (čüą╝. čĆąĖčü. 3). ą¤ąŠ ąŠčüąĖ ą░ą▒čüčåąĖčüčü ŌĆō ą▓čĆąĄą╝čÅ ą▓ čüąĄą║., ą┐ąŠ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╣ ąŠčüąĖ ŌĆō čāą│ąŠą╗ čéą░ąĮą│ą░ąČą░ ą▓ ą│čĆą░ą┤.
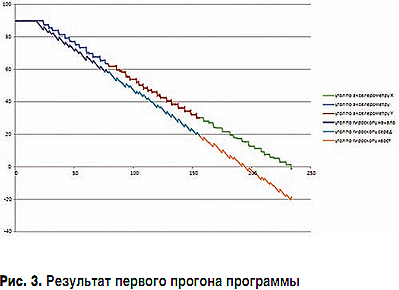
ąĪčéčāą┐ąĄąĮčīą║ąĖ, ą┐ąŠą║ą░ąĘčŗą▓ą░čÄčēąĖąĄ, čćč鹊 ą│ąŠą╗ąŠą▓ą║ą░ ą┤ą▓ąĖą│ą░ą╗ą░čüčī čĆčŗą▓ą║ą░ą╝ąĖ, ą▓ąŠąĘąĮąĖą║ą╗ąĖ ąĖąĘ-ąĘą░ ą╝ąĄčĆčéą▓ąŠą╣ ąĘąŠąĮčŗ 菹╗ąĄą║čéčĆąŠą┐čĆąĖą▓ąŠą┤ąŠą▓. ąöą╗čÅ ą▒ąŠčĆčīą▒čŗ čü ą╝ąĄčĆčéą▓ąŠą╣ ąĘąŠąĮąŠą╣ ą┐čĆąŠą│čĆą░ą╝ą╝ą░ ą▒čŗą╗ą░ ą╝ąŠą┤ąĖčäąĖčåąĖčĆąŠą▓ą░ąĮą░. ąæčŗą╗ąŠ ą▓ą▓ąĄą┤ąĄąĮąŠ čüą╗ą░ą│ą░ąĄą╝ąŠąĄ ą┤ą╗čÅ ą║ąŠą╝ą┐ąĄąĮčüą░čåąĖąĖ ą╝ąĄčĆčéą▓ąŠą╣ ąĘąŠąĮčŗ. ąóą░ą║ąŠąĄ čüą╗ą░ą│ą░ąĄą╝ąŠąĄ ą┐čĆąĖą▓ąĄą╗ąŠ ą║ ą░ą▓č鹊ą║ąŠą╗ąĄą▒ą░ąĮąĖčÅą╝ ą░ą╝ą┐ą╗ąĖčéčāą┤ąŠą╣ ąŠą║ąŠą╗ąŠ 1/8ŌĆō3/16 ą│čĆą░ą┤. ą¤čĆąĖ ąĖčģ ą▓ąŠąĘąĮąĖą║ąĮąŠą▓ąĄąĮąĖąĖ čéčĆąĄąĮąĖąĄ ą┐ąŠą║ąŠčÅ ąĮąĄ čüą║ą░ąĘčŗą▓ą░ąĄčéčüčÅ ąĖ ąĮąĄ ą▓ą╗ąĖčÅąĄčé ąĮą░ č鹊čćąĮąŠčüčéčī ąŠčéčĆą░ą▒ąŠčéą║ąĖ. ąśąĮč鹥čĆąĄčüąĮąŠ, čćč鹊 čéčĆąĄąĮąĖąĄ ą┐ąŠą║ąŠčÅ ą▓ ą┐ąŠą┤čłąĖą┐ąĮąĖą║ą░čģ čüąŠąĘą┤ą░ą▓ą░ą╗ąŠ ą┐čĆąŠą▒ą╗ąĄą╝čŗ ąĖ ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ čéčĆą░ą┤ąĖčåąĖąŠąĮąĮčŗčģ ą╝ąĄčģą░ąĮąĖč湥čüą║ąĖčģ ą│ąĖčĆąŠčüą║ąŠą┐ąŠą▓, ąŠą┤ąĮąĖą╝ ąĖąĘ čĆąĄčłąĄąĮąĖą╣ ą▒čŗą╗ąŠ ą▓ąĖą▒čĆą░čåąĖąŠąĮąĮąŠąĄ ą▓čĆą░čēąĄąĮąĖąĄ čüąĄą┐ą░čĆą░č鹊čĆą░ ą▓ čłą░čĆąĖą║ąŠą┐ąŠą┤čłąĖą┐ąĮąĖą║ą░čģ.
MEMS-ą┤ą░čéčćąĖą║ąĖ čāą│ą╗ąŠą▓ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ ą┤ąĄą╝ąŠąĮčüčéčĆąĖčĆčāčÄčé ą┤čĆąĄą╣čä ąĮčāą╗čÅ ąĖąĘ-ąĘą░ ą║ąŠą╗ąĄą▒ą░ąĮąĖą╣ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčŗ. ą¤čĆąĖ ą▓ą║ą╗čÄč湥ąĮąĖąĖ ą┤ą░čéčćąĖą║ą░ ąĮą░čćąĖąĮą░ąĄčéčüčÅ ąĄą│ąŠ čĆą░ąĘąŠą│čĆąĄą▓ ąĖąĘ-ąĘą░ čüąŠą▒čüčéą▓ąĄąĮąĮąŠą│ąŠ č鹥ą┐ą╗ąŠą▓čŗą┤ąĄą╗ąĄąĮąĖčÅ, ą┐čĆąĖ čŹč鹊ą╝ ą┐čĆąŠąĖčüčģąŠą┤ąĖčé čāčģąŠą┤ ąĮčāą╗čÅ čāą│ą╗ąŠą▓ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ. ąöą╗čÅ ą╝ą░ą╗čŗčģ čüą║ąŠčĆąŠčüč鹥ą╣ ąĖąĘą╝ąĄąĮąĄąĮąĖčÅ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčŗ čāčģąŠą┤ ą┐čĆąĖą╝ąĄčĆąĮąŠ ą┐čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗ąĄąĮ č鹥ą╝ą┐ąĄčĆą░čéčāčĆąĄ, ą┐čĆąĖ čĆąĄąĘą║ąĖčģ ąĖąĘą╝ąĄąĮąĄąĮąĖčÅčģ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčŗ čŹčéą░ ą┐čĆąŠą┐ąŠčĆčåąĖąŠąĮą░ą╗čīąĮąŠčüčéčī ąĮą░čĆčāčłą░ąĄčéčüčÅ. ąóą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝, ą┐čĆąĖ 菹║čüą┐ą╗čāą░čéą░čåąĖąĖ ą┤ą░čéčćąĖą║ą░ ąĮąĄąŠą▒čģąŠą┤ąĖą╝ąŠ ąĖąĘą▒ąĄą│ą░čéčī ą▒čŗčüčéčĆčŗčģ ąĖąĘą╝ąĄąĮąĄąĮąĖą╣ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčŗ.
ą¤ąŠčüč鹊čÅąĮąĮą░čÅ ą▓čĆąĄą╝ąĄąĮąĖ ą┐čĆąŠą│čĆąĄą▓ą░ ą│ąĖčĆąŠčüą║ąŠą┐ą░ ą▓ čüą┐ąŠą║ąŠą╣ąĮąŠą╝ ą▓ąŠąĘą┤čāčģąĄ ą▒čŗą╗ą░ 菹║čüą┐ąĄčĆąĖą╝ąĄąĮčéą░ą╗čīąĮąŠ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮą░ ąĖ čüąŠčüčéą░ą▓ąĖą╗ą░ ąŠą║ąŠą╗ąŠ 12 ą╝ąĖąĮčāčé. ą×ą▒čŗčćąĮąŠ čéčĆąĄą▒ąŠą▓ą░ą╗ąŠčüčī ąĮąĄ ą╝ąĄąĮąĄąĄ 18 ą╝ąĖąĮčāčé ąŠčé ą┐ąĄčĆą▓ąŠą│ąŠ ą▓ą║ą╗čÄč湥ąĮąĖčÅ ą┤ąŠ ą║ą░ą╗ąĖą▒čĆąŠą▓ą║ąĖ ąĮčāą╗čÅ.
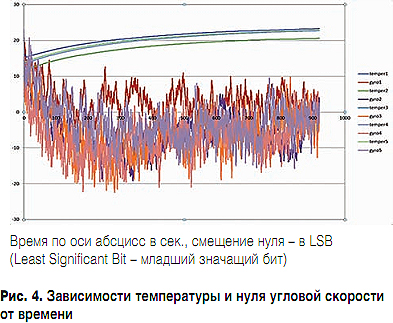
ąÜąŠčĆčĆąĄą║čåąĖčÅ ą╝ąĄą┤ą╗ąĄąĮąĮčŗčģ ąĖąĘą╝ąĄąĮąĄąĮąĖą╣ č鹥ą╝ą┐ąĄčĆą░čéčāčĆčŗ ą▒čŗą╗ą░ čĆąĄą░ą╗ąĖąĘąŠą▓ą░ąĮą░, ąĮąŠ, ą┐ąŠčüą║ąŠą╗čīą║čā ą┐čĆąĖ ą▒čŗčüčéčĆčŗčģ ąĖąĘą╝ąĄąĮąĄąĮąĖčÅčģ ąŠąĮą░ ąĮąĄ čĆą░ą▒ąŠčéą░ąĄčé, ą▓čüąĄ čĆą░ą▓ąĮąŠ čéčĆąĄą▒čāąĄčéčüčÅ ą┐ąŠą┤ąŠąČą┤ą░čéčī 15 ą╝ąĖąĮčāčé ą┤ąŠ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÅ ą┤ą░čéčćąĖą║ą░. ąØą░ ą┐čĆąĖą▓ąĄą┤ąĄąĮąĮąŠą╝ ą│čĆą░čäąĖą║ąĄ (čüą╝. čĆąĖčü. 4) ą║ąŠčĆčĆąĄą║čåąĖčÅ ą╝ąĄą┤ą╗ąĄąĮąĮčŗčģ ąĖąĘą╝ąĄąĮąĄąĮąĖą╣ čāąČąĄ ą▓ą║ą╗čÄč湥ąĮą░, ąĮąŠ ą▓ąĖą┤ąĮąŠ, čćč鹊 ąĄąĄ ą▓ą╗ąĖčÅąĮąĖąĄ ą▓ ą┐ąĄčĆą▓čŗąĄ 5 ą╝ąĖąĮčāčé čĆą░ą▒ąŠčéčŗ ąĮąĄą┤ąŠčüčéą░č鹊čćąĮąŠ.
ąØąĄčüą╝ąŠčéčĆčÅ ąĮą░ č鹊, čćč鹊 MEMS-ą│ąĖčĆąŠčüą║ąŠą┐ čÅą▓ą╗čÅąĄčéčüčÅ ą┤ą░čéčćąĖą║ąŠą╝ čāą│ą╗ąŠą▓ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ, čā ąĮąĄą│ąŠ ąĄčüčéčī ą┐ą░čĆą░ąĘąĖčéąĮą░čÅ čćčāą▓čüčéą▓ąĖč鹥ą╗čīąĮąŠčüčéčī ą║ ą╗ąĖąĮąĄą╣ąĮąŠą╝čā čāčüą║ąŠčĆąĄąĮąĖčÄ. ąŻčüą║ąŠčĆąĄąĮąĖąĄ, ąĮą░ą┐čĆą░ą▓ą╗ąĄąĮąĮąŠąĄ ą▓ą┤ąŠą╗čī ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąĮąŠą╣ ąŠčüąĖ ą│ąĖčĆąŠčüą║ąŠą┐ą░, ą▓čŗąĘčŗą▓ą░ąĄčé čüą╝ąĄčēąĄąĮąĖąĄ ąĮčāą╗čÅ, ą░ ą┐čĆąĖ ąĖąĮč鹥ą│čĆąĖčĆąŠą▓ą░ąĮąĖąĖ ŌĆō čäą░ąĮč鹊ą╝ąĮčŗą╣ ą┐ąŠą▓ąŠčĆąŠčé, čćč鹊 ąĖ ą▒čŗą╗ąŠ ą┐čĆąĖčćąĖąĮąŠą╣ čĆą░čüčģąŠąČą┤ąĄąĮąĖčÅ, ą┐ąŠą║ą░ąĘą░ąĮąĮąŠą│ąŠ ąĮą░ čĆąĖčü. 4. "ąĪčéčāą┐ąĄąĮčīą║ąĖ" ąĮą░ ą│čĆą░čäąĖą║ąĄ ąĘą░čéčĆčāą┤ąĮąĖą╗ąĖ ą┐čĆą░ą▓ąĖą╗čīąĮčāčÄ ąĖąĮč鹥čĆą┐čĆąĄčéą░čåąĖčÄ čÅą▓ą╗ąĄąĮąĖčÅ.
ąÆ čäąĖčĆą╝ąĄąĮąĮąŠą╝ čüą┐čĆą░ą▓ąŠčćąĮąŠą╝ ą╗ąĖčüč鹥 ąĮą░ ą╝ąĖą║čĆąŠčüčģąĄą╝čā ADIS16300[4] čćčāą▓čüčéą▓ąĖč鹥ą╗čīąĮąŠčüčéčī ą║ ą╗ąĖąĮąĄą╣ąĮąŠą╝čā čāčüą║ąŠčĆąĄąĮąĖčÄ čāą║ą░ąĘą░ąĮą░ ąŠą┤ąĖąĮą░ą║ąŠą▓ąŠą╣ ą┤ą╗čÅ ą▓čüąĄčģ ąŠčüąĄą╣, čćč鹊 ąĮąĄ čüąŠąŠčéą▓ąĄčéčüčéą▓čāąĄčé ąĖčüčéąĖąĮąĄ, ą┐ąŠčŹč鹊ą╝čā ą┐čĆąĖčłą╗ąŠčüčī 菹║čüą┐ąĄčĆąĖą╝ąĄąĮčéą░ą╗čīąĮąŠ ą▓čŗčÅčüąĮąĖčéčī čģą░čĆą░ą║č鹥čĆ čŹč鹊ą╣ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéąĖ. ą×ą║ą░ąĘą░ą╗ąŠčüčī, čćč鹊 ąĖ čā ADIS16300, ąĖ čā ADIS16251 čćčāą▓čüčéą▓ąĖč鹥ą╗čīąĮąŠčüčéčī ą┤ą░čéčćąĖą║ą░ čāą│ą╗ąŠą▓ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ ą║ ą╗ąĖąĮąĄą╣ąĮąŠą╝čā čāčüą║ąŠčĆąĄąĮąĖčÄ ą╝ą░ą║čüąĖą╝ą░ą╗čīąĮą░ ą▓ą┤ąŠą╗čī ąŠčüąĖ Y ąĖ ą┐čĆą░ą║čéąĖč湥čüą║ąĖ ąŠčéčüčāčéčüčéą▓čāąĄčé ą▓ą┤ąŠą╗čī ąŠčüąĖ X. ą¤ąŠ ąŠčüąĖ Z, čÅą▓ą╗čÅčÄčēąĄą╣čüčÅ ąŠčüčīčÄ ąĖąĘą╝ąĄčĆąĄąĮąĖčÅ čāą│ą╗ąŠą▓ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ, ąŠąĮą░ ą┐čĆąŠą╝ąĄąČčāč鹊čćąĮą░čÅ. ąÜą░ą║ čüą╗ąĄą┤čüčéą▓ąĖąĄ, ąĄčüą╗ąĖ ą│ąĖčĆąŠčüą║ąŠą┐ čāčüčéą░ąĮąŠą▓ąĖčéčī ą▓ čĆą░ą║ąĄč鹥 čéą░ą║, čćč鹊ą▒čŗ ą┐čĆąŠą┤ąŠą╗čīąĮąŠąĄ čāčüą║ąŠčĆąĄąĮąĖąĄ ą▒čŗą╗ąŠ ąĮą░ą┐čĆą░ą▓ą╗ąĄąĮąŠ ą▓ą┤ąŠą╗čī ąŠčüąĖ X, č鹊 ąĮąŠčĆą╝ą░ą╗čīąĮčŗą╣ ą┐ąŠą╗ąĄčé čĆą░ą║ąĄčéčŗ ąĮąĄ ą▒čāą┤ąĄčé čüą║ą░ąĘčŗą▓ą░čéčīčüčÅ ąĮą░ ą┐ąŠą║ą░ąĘą░ąĮąĖčÅčģ ą│ąĖčĆąŠčüą║ąŠą┐ą░, ąĖ ą▓ą╗ąĖčÅąĮąĖąĄ ą┐ą░čĆą░ąĘąĖčéąĮąŠą╣ čćčāą▓čüčéą▓ąĖč鹥ą╗čīąĮąŠčüčéąĖ ą▒čāą┤ąĄčé ąĮąĄą▓ąĄą╗ąĖą║ąŠ. ąÆ ą╝ąŠą┤ąĄą╗čīąĮąŠą╣ čāčüčéą░ąĮąŠą▓ą║ąĄ ą▓ ąĮą░čćą░ą╗ąĄ čĆą░ąĘą▓ąŠčĆąŠčéą░ ą┐ąŠ čéą░ąĮą│ą░ąČčā ą│ąĖčĆąŠčüą║ąŠą┐ ąĘą░ąĮąĖą╝ą░ąĄčé ąĮą░ąĖą▓čŗą│ąŠą┤ąĮąĄą╣čłąĄąĄ ą┐ąŠą╗ąŠąČąĄąĮąĖąĄ, ą┐čĆąĖ ą║ąŠč鹊čĆąŠą╝ ą▓ą╗ąĖčÅąĮąĖąĄ čāčüą║ąŠčĆąĄąĮąĖčÅ čüą▓ąŠą▒ąŠą┤ąĮąŠą│ąŠ ą┐ą░ą┤ąĄąĮąĖčÅ ą╝ąĖąĮąĖą╝ą░ą╗čīąĮąŠ. ą¤ąŠ ą╝ąĄčĆąĄ ą┐ąŠą▓ąŠčĆąŠčéą░ ą┐čĆąŠąĄą║čåąĖčÅ ą▓ąĄą║č鹊čĆą░ g ąĮą░ ąŠčüčī Y čāą▓ąĄą╗ąĖčćąĖą▓ą░ąĄčéčüčÅ, ąĖ ą┐ąŠ ą╝ąĄčĆąĄ čāą▓ąĄą╗ąĖč湥ąĮąĖčÅ ąĮąŠą╗čī čāą│ą╗ąŠą▓ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ ą│ąĖčĆąŠčüą║ąŠą┐ą░ čüą╝ąĄčēą░ąĄčéčüčÅ. ąŁč鹊 ą▓ąŠčüą┐čĆąĖąĮąĖą╝ą░ąĄčéčüčÅ ą║ą░ą║ ąĖąĘą╝ąĄąĮąĄąĮąĖąĄ čāą│ą╗ąŠą▓ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ. ąÆ čĆąĄąĘčāą╗čīčéą░č鹥 ą┐čĆąĖ ą┐ąŠčüč鹊čÅąĮąĮąŠą╣, ą┐ąŠ ą┤ą░ąĮąĮčŗą╝ ą│ąĖčĆąŠčüą║ąŠą┐ą░, čāą│ą╗ąŠą▓ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ ą┐čĆąŠąĖčüčģąŠą┤ąĖčé čäą░ą║čéąĖč湥čüą║ąŠąĄ ąĘą░ą╝ąĄą┤ą╗ąĄąĮąĖąĄ ą┐ąŠą▓ąŠčĆąŠčéą░.
ąØąĄčüą╝ąŠčéčĆčÅ ąĮą░ č鹊, čćč鹊 čŹč鹊 čÅą▓ą╗ąĄąĮąĖąĄ ąĮąĄ ą▒čāą┤ąĄčé ąĖą╝ąĄčéčī ą╝ąĄčüčéą░ ąĮą░ ą▒ąŠčĆčéčā čĆą░ą║ąĄčéčŗ, čé.ą║. čéą░ą╝ ąŠčéą║ą╗ąŠąĮąĄąĮąĖąĄ ą▓ąĄą║č鹊čĆą░ čāčüą║ąŠčĆąĄąĮąĖčÅ ąŠčé ą┐čĆąŠą┤ąŠą╗čīąĮąŠą╣ ąŠčüąĖ čĆą░ą║ąĄčéčŗ ąĮąĖčćč鹊ąČąĮąŠ, ą┤ą╗čÅ ąŠčåąĄąĮą║ąĖ č鹊čćąĮąŠčüčéąĮčŗčģ čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ ą▓ ą╝ą░ą║ąĄč鹥 ą┐ąŠčéčĆąĄą▒ąŠą▓ą░ą╗ąŠčüčī ą▓ą▓ąĄčüčéąĖ čéą░ą║čāčÄ ą║ąŠčĆčĆąĄą║čåąĖčÄ. ąöą╗čÅ ą╗ąĄčéąĮąŠą╣ čüąĖčüč鹥ą╝čŗ čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ ą║ąŠčĆčĆąĄą║čåąĖčÅ ą▒čāą┤ąĄčé ąĮąĄąŠą▒čģąŠą┤ąĖą╝ą░ ą┤ą╗čÅ ą│ąĖčĆąŠčüą║ąŠą┐ą░, ąĖąĘą╝ąĄčĆčÅčÄčēąĄą│ąŠ čāą│ą╗ąŠą▓čāčÄ čüą║ąŠčĆąŠčüčéčī ą┐ąŠ ą║čĆąĄąĮčā, čé.ą║. ąŠąĮ ąĮąĄ ą╝ąŠąČąĄčé ą▒čŗčéčī čüąŠčĆąĖąĄąĮčéąĖčĆąŠą▓ą░ąĮ "ą▓čŗą│ąŠą┤ąĮąŠą╣" ąŠčüčīčÄ X ą▓ą┤ąŠą╗čī ą┐čĆąŠą┤ąŠą╗čīąĮąŠą│ąŠ čāčüą║ąŠčĆąĄąĮąĖčÅ. ą¤ąŠčüą╗ąĄ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖčÅ ą┐čĆąŠčåąĄą┤čāčĆ ą║ąŠčĆčĆąĄą║čåąĖąĖ ą┐ąŠ č鹥ą╝ą┐ąĄčĆą░čéčāčĆąĄ ąĖ ą┐ąŠ ą╗ąĖąĮąĄą╣ąĮąŠą╝čā čāčüą║ąŠčĆąĄąĮąĖčÄ ą┤ą░ąĮąĮčŗąĄ ą┐čĆąŠą│ąŠąĮąŠą▓ čüčéą░ą╗ąĖ čüąŠąŠčéą▓ąĄčéčüčéą▓ąŠą▓ą░čéčī ąĘą░čÅą▓ą╗ąĄąĮąĮčŗą╝ ą▓ ą┤ą░čéą░čłąĖč鹥 čģą░čĆą░ą║č鹥čĆąĖčüčéąĖą║ą░ą╝ ą│ąĖčĆąŠčüą║ąŠą┐ą░ ą┐ąŠ ą┐ąŠą▓č鹊čĆčÅąĄą╝ąŠčüčéąĖ ąĖ ą▓ą░čĆąĖą░čåąĖąĖ ąÉą╗ą╗ą░ąĮą░.
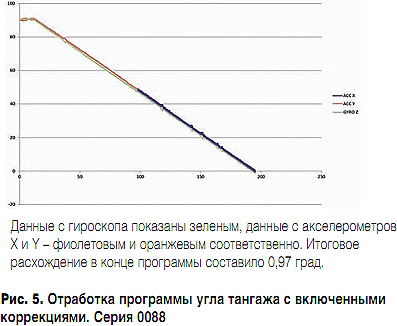
ą¤ąŠ čĆąĄąĘčāą╗čīčéą░čéą░ą╝ 100 ą┐čĆąŠą│ąŠąĮąŠą▓ ąŠą┐čĆąĄą┤ąĄą╗ąĄąĮąŠ čüčĆąĄą┤ąĮąĄą║ą▓ą░ą┤čĆą░čéąĖčćąĮąŠąĄ ąĘąĮą░č湥ąĮąĖąĄ ąŠčłąĖą▒ą║ąĖ ąĮą░ 190-ą╣ čüąĄą║. ą┐čĆąŠą│čĆą░ą╝ą╝čŗ ą▓ 1,5 ą│čĆą░ą┤. čüąŠ čüčéą░ąĮą┤ą░čĆčéąĮčŗą╝ ąŠčéą║ą╗ąŠąĮąĄąĮąĖąĄą╝ σ = 1,5 ą│čĆą░ą┤. ą¤čĆąĖ čŹč鹊ą╝ 0,25 ąĖąĘ 1,5 ą│čĆą░ą┤. ą╝ąŠą│čāčé ą▒čŗčéčī "čüą┐ąĖčüą░ąĮčŗ" ąĮą░ ąĮąĄą┐ąĄčĆą┐ąĄąĮą┤ąĖą║čāą╗čÅčĆąĮąŠčüčéčī ąŠčüąĄą╣ ą│ąĖčĆąŠčüą║ąŠą┐ą░ ąĖ ą░ą║čüąĄą╗ąĄčĆąŠą╝ąĄčéčĆą░ Y.
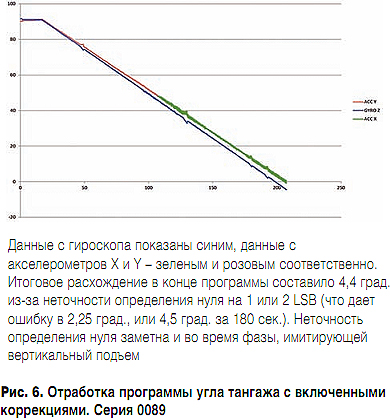
ąØą░ čĆąĖčü. 5 ąĖ 6 ą┐čĆąĄą┤čüčéą░ą▓ą╗ąĄąĮčŗ čéąĖą┐ąĖčćąĮčŗąĄ ą│čĆą░čäąĖą║ąĖ čĆą░ą▒ąŠčéčŗ čāčüčéą░ąĮąŠą▓ą║ąĖ ą┐čĆąĖ ą▓ą║ą╗čÄč湥ąĮąĮčŗčģ ą║ąŠčĆčĆąĄą║čåąĖčÅčģ.
ąöą╗čÅ ą╝ąŠą┤ąĄą╗ąĖčĆąŠą▓ą░ąĮąĖčÅ čäą░ą║čéąĖč湥čüą║ąĖąĄ ą▓ąĄą╗ąĖčćąĖąĮčŗ čāą│ą╗ą░ čéą░ąĮą│ą░ąČą░ ą┐ąŠą┤čüčéą░ą▓ą╗čÅą╗ąĖčüčī ą▓ čüą┐čĆąĄą┤čłąĖčé Launchmodel, ąĖ ą┐ą░čĆą░ą╝ąĄčéčĆčŗ ą┐ąŠą╗čāčćąĖą▓čłąĄą╣čüčÅ ąŠčĆą▒ąĖčéčŗ čüčĆą░ą▓ąĮąĖą▓ą░ą╗ąĖčüčī čü ąĖą┤ąĄą░ą╗čīąĮčŗą╝ąĖ. ą”ąĄą╗ąĄą▓čŗąĄ ąŠčĆą▒ąĖčéčŗ ą▓čŗą▒ąĖčĆą░ą╗ąĖčüčī ąĮąĖąĘą║ąĖą╝ąĖ, čé.ą║. ąĮą░ ąĮąĖčģ ą▒ąŠą╗čīčłąĄ ąĘą░ą╝ąĄčéąĮąŠ ą▓ą╗ąĖčÅąĮąĖąĄ ą░čŹčĆąŠą┤ąĖąĮą░ą╝ąĖč湥čüą║ąĖčģ ą┐ąŠč鹥čĆčī, ą░ ą│čĆčāąĘąŠą┐ąŠą┤čŖąĄą╝ąĮąŠčüčéčī ąĮą░ąĮąŠąĮąŠčüąĖč鹥ą╗čÅ čāą▓ąĄą╗ąĖčćąĖą▓ą░ą╗ą░čüčī.
ą¤čĆąĖčåąĄą╗ąĖą▓ą░ąĮąĖąĄ ą┐ąŠ ąĪąŠą╗ąĮčåčā ą┐ąŠąĘą▓ąŠą╗čÅąĄčé čāą╝ąĄąĮčīčłąĖčéčī ą▓ ąĮąĄčüą║ąŠą╗čīą║ąŠ čĆą░ąĘ čāą│ą╗ąŠą▓čāčÄ ąŠčłąĖą▒ą║čā ą┐ąĄčĆąĄą┤ ąĘą░ą┐čāčüą║ąŠą╝ ą▓ąĄčĆčģąĮąĖčģ čüčéčāą┐ąĄąĮąĄą╣, ąĮąŠ ąĮąĄ ą┐ąŠą│čĆąĄčłąĮąŠčüčéąĖ ą▓ čåąĄą╗ąŠą╝.
ą×ą║ą░ąĘčŗą▓ą░ąĄčéčüčÅ ą▓čŗą│ąŠą┤ąĮčŗą╝ ą┐ąŠčüčéą░ą▓ąĖčéčī ą┤ą╗ąĖč鹥ą╗čīąĮąŠčüčéčī ą▒ą░ą╗ą╗ąĖčüčéąĖč湥čüą║ąŠą╣ ą┐ą░čāąĘčŗ ą▓ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī ąŠčé čäą░ą║čéąĖč湥čüą║ąŠą╣ čüą║ąŠčĆąŠčüčéąĖ čĆą░ąĘą▓ąŠčĆąŠčéą░ ą┐ąŠ čéą░ąĮą│ą░ąČčā, ą║ąŠč鹊čĆą░čÅ ą╝ąŠąČąĄčé ą▒čŗčéčī ąĖąĘą╝ąĄčĆąĄąĮą░ ą┐ąŠ ą▓čĆąĄą╝ąĄąĮąĖ ą┐čĆąĖčģąŠą┤ą░ ąĪąŠą╗ąĮčåą░ ą▓ ą┐ąŠą╗ąĄ ąĘčĆąĄąĮąĖčÅ čüąŠą╗ąĮąĄčćąĮąŠą│ąŠ ą┤ą░čéčćąĖą║ą░, č鹊ą│ą┤ą░ ą╝ąŠąČąĮąŠ ą┤ąŠą▒ąĖčéčīčüčÅ, čćč鹊ą▒čŗ ą┐ąĄčĆąĖą│ąĄą╣ ą▒čŗą╗ ąĮąĄ ąĮąĖąČąĄ č鹥čĆą╝ąĖąĮą░ą╗čīąĮąŠą╣ č鹊čćą║ąĖ.
ą¤čĆąĖ čŹč鹊ą╝ ą▓čŗčüąŠčéą░ ą░ą┐ąŠą│ąĄčÅ ąĖąĘą╝ąĄąĮčÅąĄčéčüčÅ ąĘąĮą░čćąĖč鹥ą╗čīąĮąŠ ą▒ąŠą╗čīčłąĄ, č湥ą╝ ą▓čŗčüąŠčéą░ ą┐ąĄčĆąĖą│ąĄčÅ, ą┐ąŠčüą║ąŠą╗čīą║čā ą▓ąĄčĆčģąĮąĖąĄ čüčéčāą┐ąĄąĮąĖ ąŠą┐ąĖčüčŗą▓ą░ąĄą╝ąŠą╣ ą╝ąŠą┤ąĄą╗ąĖ ąĮąĄ ąĖą╝ąĄčÄčé ą▓ąŠąĘą╝ąŠąČąĮąŠčüčéąĖ ąŠčéčüąĄčćą║ąĖ ąĖ ą▓čüąĄą│ą┤ą░ čĆą░ą▒ąŠčéą░čÄčé ą┤ąŠ ą┐ąŠą╗ąĮąŠą╣ ą▓čŗčĆą░ą▒ąŠčéą║ąĖ č鹊ą┐ą╗ąĖą▓ą░. ąśąĘą╝ąĄąĮąĄąĮąĖąĄ ą▓čŗčüąŠčéčŗ ą┐ąĄčĆąĖą│ąĄčÅ ąĮą░ 1 ą║ą╝ ą┐čĆąĖą▓ąŠą┤ąĖčé ą║ ąĖąĘą╝ąĄąĮąĄąĮąĖčÄ ą▓čŗčüąŠčéčŗ ą░ą┐ąŠą│ąĄčÅ ąĮą░ 10ŌĆō12 ą║ą╝. ąØą░ čĆąĖčü. 7 ą┐čĆąĖą▓ąĄą┤ąĄąĮą░ ąĘą░ą▓ąĖčüąĖą╝ąŠčüčéčī ą▓čŗčüąŠčé ą┐ąĄčĆąĖą│ąĄčÅ ąĖ ą░ą┐ąŠą│ąĄčÅ, ą░ čéą░ą║ąČąĄ ąŠą┐čéąĖą╝ą░ą╗čīąĮąŠą╣ ą┤ą╗ąĖč鹥ą╗čīąĮąŠčüčéąĖ ą▒ą░ą╗ą╗ąĖčüčéąĖč湥čüą║ąŠą╣ ą┐ą░čāąĘčŗ ą┤ą╗čÅ čĆą░čüčüą╝ą░čéčĆąĖą▓ą░ąĄą╝ąŠą╣ ą│ąĖą┐ąŠč鹥čéąĖč湥čüą║ąŠą╣ čĆą░ą║ąĄčéčŗ.
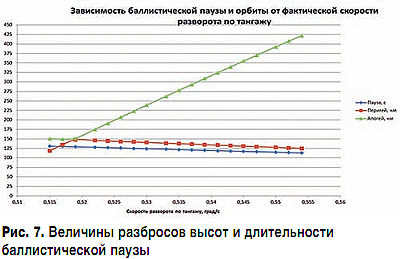
ąĪą╗ąĄą┤čāąĄčé ąŠčéą╝ąĄčéąĖčéčī, čćč鹊 ą▓čüčÅ ąŠč鹊ą▒čĆą░ąČą░ąĄą╝ą░čÅ ą┐ąŠ ąŠčüąĖ ą░ą▒čüčåąĖčüčü ąŠą▒ą╗ą░čüčéčī (ąŠčé 0,51 ą│čĆą░ą┤./c ą┤ąŠ 0,56 ą│čĆą░ą┤./c) ŌĆō čŹč鹊 ąŠčéą║ą╗ąŠąĮąĄąĮąĖąĄ ┬▒2 LSB ą┤ą░čéčćąĖą║ą░ ADIS16300, čéą░ą║ąĖą╝ ąŠą▒čĆą░ąĘąŠą╝, ą┤ą░ąČąĄ čü ą║ąŠčĆčĆąĄą║čåąĖąĄą╣ ą┐ąŠ ąĪąŠą╗ąĮčåčā ą▓čŗą▓ąĄą┤ąĄąĮąĖąĄ ąĮą░ ąŠčĆą▒ąĖčéčā čü čéą░ą║ąĖą╝ ąĮąĖąĘą║ąĖą╝ ą┐ąĄčĆąĖą│ąĄąĄą╝ ąĮą░čģąŠą┤ąĖčéčüčÅ ąĮą░ ą┐čĆąĄą┤ąĄą╗ąĄ č鹊čćąĮąŠčüčéąĮčŗčģ ą▓ąŠąĘą╝ąŠąČąĮąŠčüč鹥ą╣ čŹč鹊ą│ąŠ ą│ąĖčĆąŠčüą║ąŠą┐ą░. ąĢčüą╗ąĖ, ąŠą┤ąĮą░ą║ąŠ, čāą╝ąĄąĮčīčłąĖčéčī ą▓ąĄą╗ąĖčćąĖąĮčā ą┐ąŠą╗ąĄąĘąĮąŠą╣ ąĮą░ą│čĆčāąĘą║ąĖ ąĖ ą▓čŗą▒čĆą░čéčī ąŠčĆą▒ąĖčéčā čü ą▒ąŠą╗ąĄąĄ ą▓čŗčüąŠą║ąĖą╝ ą┐ąĄčĆąĖą│ąĄąĄą╝ (240ŌĆō300 ą║ą╝), č鹊 ą┤ąĖą░ą┐ą░ąĘąŠąĮ ą▓ąŠąĘą╝ąŠąČąĮčŗčģ ąŠčłąĖą▒ąŠą║, ą┐čĆąĖ ą║ąŠč鹊čĆčŗčģ ą▓čŗą▓ąĄą┤ąĄąĮąĖąĄ ąĮą░ čüčéą░ą▒ąĖą╗čīąĮčāčÄ ąŠčĆą▒ąĖčéčā (ą┐čāčüčéčī ąĖ ąŠčéą╗ąĖčćą░čÄčēčāčÄčüčÅ ąŠčé čåąĄą╗ąĄą▓ąŠą╣ ą▓ ąĮąĄą║ąŠč鹊čĆąŠą╣ čüč鹥ą┐ąĄąĮąĖ), ąĘą░ą╝ąĄčéąĮąŠ čāą▓ąĄą╗ąĖčćąĖčéčüčÅ.
ąöą╗čÅ ąŠčåąĄąĮą║ąĖ ą▓ą╗ąĖčÅąĮąĖčÅ ą▓ąĖą▒čĆą░čåąĖą╣ ąĮą░ č鹊čćąĮąŠčüčéčī ą┤ą░čéčćąĖą║ąŠą▓ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ą╗čüčÅ čüą░ą╝ąŠą┤ąĄą╗čīąĮčŗą╣ ą▓ąĖą▒čĆąŠčüč鹥ąĮą┤ ąĖąĘ čüą░ą▒ą▓čāč乥čĆą░ ąĖ čāčüąĖą╗ąĖč鹥ą╗čÅ ą╝ąŠčēąĮąŠčüčéąĖ ąĘą▓čāą║ąŠą▓ąŠą╣ čćą░čüč鹊čéčŗ (ąŻą£ąŚą¦), ąŠą▒ąĄčüą┐ąĄčćąĖą▓ą░čÄčēąĖą╣ ą░ą╝ą┐ą╗ąĖčéčāą┤čā ą▓ąĖą▒čĆą░čåąĖąŠąĮąĮąŠą│ąŠ čāčüą║ąŠčĆąĄąĮąĖčÅ ą┤ąŠ 25 g ąĮą░ čćą░čüč鹊č鹥 40 ąōčå. ąŻčüą║ąŠčĆąĄąĮąĖąĄ ą║ąŠąĮčéčĆąŠą╗ąĖčĆąŠą▓ą░ą╗ąŠčüčī ą┐ąŠ ą▓ąĮąĄčłąĮąĄą╝čā ą░ą║čüąĄą╗ąĄčĆąŠą╝ąĄčéčĆčā ADXL150, čéą░ą║ ą║ą░ą║ ą▓čüčéčĆąŠąĄąĮąĮčŗą╣ ą░ą║čüąĄą╗ąĄ čĆąŠą╝ąĄ čé čĆ ADIS16300 ąĖą╝ąĄąĄčé ą┤ąĖą░ą┐ą░ąĘąŠąĮ č鹊ą╗čīą║ąŠ ą┤ąŠ 3,5 g.
ąŚąĮą░čćąĖą╝ąŠą│ąŠ ą▓ą╗ąĖčÅąĮąĖčÅ ą┐ąŠ ąŠčüąĖ X ąĮą░ ą▓čŗčģąŠą┤ąĮąŠą╣ čüąĖą│ąĮą░ą╗ ą│ąĖčĆąŠčüą║ąŠą┐ą░ ąĮąĄ ąŠą▒ąĮą░čĆčāąČąĄąĮąŠ. ąÆą╗ąĖčÅąĮąĖąĄ ą┐ąŠ ąŠčüčÅą╝ Y ąĖ Z ą▓ ą┤ąĖą░ą┐ą░ąĘąŠąĮąĄ ą┤ąŠ 10 g ą╗ąĖąĮąĄą╣ąĮąŠ čü č鹊čćąĮąŠčüčéčīčÄ ąĮąĄ čģčāąČąĄ 1%, ą┐ąŠčŹč鹊ą╝čā ąĮą░ ąĘąĮą░č湥ąĮąĖąĖ ąĖąĮč鹥ą│čĆą░ą╗ą░ ąŠą▒ąĮą░čĆčāąČąĖą╝ąŠ ąĮąĄ čüą║ą░ąĘčŗą▓ą░ąĄčéčüčÅ. ą×ą▒čŖąĄą╝ ąĖčüą┐čŗčéą░ąĮąĖą╣ ąĮą░ ą▓ąĖą▒čĆąŠčüč鹥ąĮą┤ąĄ ą▒čŗą╗ąŠ čĆąĄčłąĄąĮąŠ čüąŠą║čĆą░čéąĖčéčī, čéą░ą║ ą║ą░ą║ ą▒čŗą╗ąŠ ąŠą▒ąĮą░čĆčāąČąĄąĮąŠ, čćč鹊 ą▓ąĖą▒čĆą░čåąĖčÅ ą▓ąĄą╗ąĖčćąĖąĮąŠą╣ ~0,5 ą╝/čü2, ą▓ąŠąĘąĮąĖą║ą░čÄčēą░čÅ ą▓ čĆą░ą▒ąŠč湥ą╝ čĆąĄąČąĖą╝ąĄ, ąĮą░ č鹊čćąĮąŠčüčéąĖ ąĮąĄ čüą║ą░ąĘčŗą▓ą░ąĄčéčüčÅ, ą░ ą▓čģąŠąČą┤ąĄąĮąĖąĄ ą░ą║čüąĄą╗ąĄčĆąŠą╝ąĄčéčĆą░ ą▓ ąŠą│čĆą░ąĮąĖč湥ąĮąĖąĄ ąĮąĄ ą▓ą╗ąĖčÅąĄčé ąĮą░ č鹊čćąĮąŠčüčéčī ą┐ąŠą║ą░ąĘą░ąĮąĖą╣ ą│ąĖčĆąŠčüą║ąŠą┐ą░ ą▓ą┐ą╗ąŠčéčī ą┤ąŠ 10 g.
ą¤čĆąŠą▓ąĄą┤ąĄąĮąĮčŗąĄ 菹║čüą┐ąĄčĆąĖą╝ąĄąĮčéčŗ ą┐ąŠą║ą░ąĘą░ą╗ąĖ, čćč鹊 ą┤ą╗čÅ čĆą░ą║ąĄčéčŗ čü ąŠč湥ąĮčī ą║ąŠčĆąŠčéą║ąĖą╝ ą░ą║čéąĖą▓ąĮčŗą╝ čāčćą░čüčéą║ąŠą╝ ą┐čĆąĖą╝ąĄąĮąĄąĮąĖąĄ ą┤ą░čéčćąĖą║ą░ čüąŠ čüą▓ąŠą╣čüčéą▓ą░ą╝ąĖ ADIS16300 ą┐ąŠ č鹊čćąĮąŠčüčéąĖ ąĖ čāčüč鹊ą╣čćąĖą▓ąŠčüčéąĖ ą║ ą▓ąĖą▒čĆą░čåąĖąĖ ąĖ ą┐ąĄčĆąĄą│čĆčāąĘą║ąĄ ą┐ąŠąĘą▓ąŠą╗čÅąĄčé čüąŠąĘą┤ą░čéčī čüąĖčüč鹥ą╝čā čāą┐čĆą░ą▓ą╗ąĄąĮąĖčÅ, čĆąĄčłą░čÄčēčāčÄ ąĘą░ą┤ą░čćčā ą▓čŗčģąŠą┤ą░ ąĮą░ ąŠčĆą▒ąĖčéčā ą┐čĆąĖ ą▓ąĄčĆčéąĖą║ą░ą╗čīąĮąŠą╝ čüčéą░čĆč鹥. ą¤čĆąĖ čŹč鹊ą╝ čüą╗ąĄą┤čāąĄčé čāą┤ąĄą╗ąĖčéčī ą▓ąĮąĖą╝ą░ąĮąĖąĄ č鹥čĆą╝ąŠčüčéą░ą▒ąĖą╗ąĖąĘą░čåąĖąĖ ą┤ą░čéčćąĖą║ą░ ą▓ čüąŠčüčéą░ą▓ąĄ ąĪąŻ, ą┐čĆą░ą▓ąĖą╗čīąĮąŠą╣ ąĄą│ąŠ ąŠčĆąĖąĄąĮčéą░čåąĖąĖ (ąŠčüčīčÄ ąź ą┐ąŠ ą┐čĆąŠą┤ąŠą╗čīąĮąŠą╣ ąŠčüąĖ čĆą░ą║ąĄčéčŗ), ą░ čéą░ą║ąČąĄ ą░ą┤ąĄą║ą▓ą░čéąĮąŠą╣ ą┐čĆąŠą│čĆą░ą╝ą╝ąĮąŠą╣ ąŠą▒čĆą░ą▒ąŠčéą║ąĄ ą┤ą░ąĮąĮčŗčģ. ą¢ąĄą╗ą░č鹥ą╗čīąĮąŠ ąĖą╝ąĄčéčī ą╝ąĄąĮčīčłčāčÄ ą┤ąĖčüą║čĆąĄčéąĮąŠčüčéčī ą▓čŗčģąŠą┤ąĮčŗčģ ą┤ą░ąĮąĮčŗčģ, čćč鹊 ą╝ąŠąČąĄčé ąŠą▒ą╗ąĄą│čćąĖčéčī ą║ą░ą╗ąĖą▒čĆąŠą▓ą║čā ąĮčāą╗čÅ. ąŁč鹊 ą┤ąŠčüčéąĖąČąĖą╝ąŠ ą▓ ą┤ą░čéčćąĖą║ąĄ čüą╗ąĄą┤čāčÄčēąĄą│ąŠ ą┐ąŠą║ąŠą╗ąĄąĮąĖčÅ ADIS16445 ąĖą╗ąĖ ą┐čĆąĖ ąĖčüą┐ąŠą╗čīąĘąŠą▓ą░ąĮąĖąĖ ą┤ą░čéčćąĖą║ą░ čü ą░ąĮą░ą╗ąŠą│ąŠą▓čŗą╝ ą▓čŗčģąŠą┤ąŠą╝, ąĮą░ą┐čĆąĖą╝ąĄčĆ ADXRS646-EP, čüąŠą▓ą╝ąĄčüčéąĮąŠ čü 16-čĆą░ąĘčĆčÅą┤ąĮčŗą╝ ąÉą”ą¤.
ąöą╗čÅ čĆą░ą║ąĄčé čü čéąĖą┐ąĖčćąĮčŗą╝ąĖ ą┐ą░čĆą░ą╝ąĄčéčĆą░ą╝ąĖ ą░ą║čéąĖą▓ąĮąŠą│ąŠ čāčćą░čüčéą║ą░, ąŠčüąŠą▒ąĄąĮąĮąŠ ŌĆō ą╝ąĮąŠą│ąŠčüčéčāą┐ąĄąĮčćą░čéčŗčģ ąČąĖą┤ą║ąŠčüčéąĮčŗčģ, č鹊čćąĮąŠčüčéčī ADIS16300 ąĮąĄą┤ąŠčüčéą░č鹊čćąĮą░ ąĖ čéčĆąĄą▒čāąĄčé ą┤ąŠą┐ąŠą╗ąĮąĖč鹥ą╗čīąĮąŠą╣ ą║ąŠčĆčĆąĄą║čåąĖąĖ, ąĮą░ą┐čĆąĖą╝ąĄčĆ čü ą┐ąŠą╝ąŠčēčīčÄ ąŠą┤ąĮąŠąŠčüąĮąŠą╣ čüąŠą╗ąĮąĄčćąĮąŠą╣ ąŠčĆąĖąĄąĮčéą░čåąĖąĖ. ąÜ čüąŠąČą░ą╗ąĄąĮąĖčÄ, ąŠą▒čŖąĄą╝ čüčéą░čéčīąĖ ąĮąĄ ą┐ąŠąĘą▓ąŠą╗ąĖą╗ ą▓ą║ą╗čÄčćąĖčéčī ą▓ ąĮąĄąĄ ąŠą┐ąĖčüą░ąĮąĖąĄ čĆą░ą▒ąŠčéčŗ čü ą┤ą░čéčćąĖą║ąŠą╝ čüąŠą╗ąĮčåą░, čģąŠčéčÅ ą▓ čüąŠčüčéą░ą▓ąĄ čāčüčéą░ąĮąŠą▓ą║ąĖ ą┤ą░čéčćąĖą║ ą▒čŗą╗.
ą¤ą░čĆą░ą╝ąĄčéčĆčŗ č鹊čćąĮąŠčüčéąĖ, ąŠą│čĆą░ąĮąĖčćąĖą▓ą░ąĄą╝čŗąĄ ą┤ą░čéčćąĖą║ąŠą╝:
ąøąĖč鹥čĆą░čéčāčĆą░
ą×ą┐čāą▒ą╗ąĖą║ąŠą▓ą░ąĮąŠ: ą¢čāčĆąĮą░ą╗ "ąóąĄčģąĮąŠą╗ąŠą│ąĖąĖ ąĖ čüčĆąĄą┤čüčéą▓ą░ čüą▓čÅąĘąĖ" #3, 2016
ą¤ąŠčüąĄčēąĄąĮąĖą╣: 6599
ąÉą▓č鹊čĆ
| |||
ąÆ čĆčāą▒čĆąĖą║čā "ąĪą┐čāčéąĮąĖą║ąŠą▓ą░čÅ čüą▓čÅąĘčī" | ąÜ čüą┐ąĖčüą║čā čĆčāą▒čĆąĖą║ | ąÜ čüą┐ąĖčüą║čā ą░ą▓č鹊čĆąŠą▓ | ąÜ čüą┐ąĖčüą║čā ą┐čāą▒ą╗ąĖą║ą░čåąĖą╣