В рубрику "Решения операторского класса" | К списку рубрик | К списку авторов | К списку публикаций
Статья состоит из двух частей. В части 1 рассматривались теоретические положения FDM и возможность повышения спектральной эффективности системы за счет использования N-OFDM, то есть неортогонального частотного мультиплексирования сигналов на основе принципов FDM. Анализируются проблемы реализации N-OFDM и пути их решения. Представлен алгоритм демодуляции сигналов N-OFDM. В части 2 исследуется реализуемость N-OFDM на основе анализа оценок среднеквадратических ошибок при измерениях квадратурных составляющих сигналов.
The article consists of two parts. FDM theoretical aspects and the possibility of the improvement of the spectral efficiency of the system by using N-OFDM (Non-Orthogonal Frequency Division Multiplexing which is based on the FDM principles) were examined in the first part of the article. The problems of N-OFDM realization and ways of its solution are analyzed. The algorithm of demodulation of the N-OFDM signals is described. The second part of the article is about N-OFDM adoption which is based on the analysis of the mean-square errors during measurement of the quadrature components of signals.
Продолжаем рассказ о неортогональном частотном мультиплексировании сигналов (N-OFDM) (начало в предыдущем номере, с. 61–65). Вторая часть статьи посвящена анализу возможностей частотного уплотнения сигналов N-OFDM. При этом в качестве показателя эффективности демодуляции сигналов N-OFDM выбраны оценки среднеквадратических ошибок, возникающих при измерениях квадратурных составляющих амплитуд сигналов.
Основным показателем эффективности рассмотренных методов демодуляции N-OFDM-сигналов является точность оценивания квадратурных составляющих их амплитуд, характеризуемая, например, среднеквадратическим отклонением (СКО) соответствующих оценок. Опираясь на данный показатель, можно получить все остальные известные показатели качества функционирования средств связи, так или иначе базирующиеся на величине СКО. В частности, на этой основе могут быть получены вероятности ошибок и связанные с ними характеристики энергетической эффективности. По отношению к ним показатель в виде СКО оценок амплитудных компонент является первичным, и поэтому в данной статье ему будет уделено основное внимание.
Существует множество различных подходов к аналитической оценке потенциально достижимых СКО. Пожалуй, наиболее полный обзор их приведен в [19]. В частности, там отмечается возможность применения системы нижних границ Баранкина, Бхаттачария, Крамера – Рао и других.
Нижняя граница Бхаттачария предложена в 1946 г. [20]. Следует отметить, что первый ее порядок совпадает с границей Крамера – Рао [19], а при втором порядке и выше (k≥2) отличается от нее более сложными зависимостями, связанными с необходимостью обращения матрицы в k раз большей размерности. При этом сама граница Бхаттачария k-го порядка проходит выше границы Крамера – Рао и соответствует оценкам, обращающим в ноль частную производную k-го порядка от решающей функции в точке ее экстремума.
Нижняя граница Баранкина (предложена в 1949 г. [20]) характеризует дисперсию локально наилучшей оценки в заданной точке при условии несмещенности оценки в конечном числе заданных точек. Как отмечено в [19], наиболее важным и практически нерешенным вопросом, возникающим при применении границ Баранкина, является выбор указанного множества точек контроля несмещенности оценки. На практике эти точки, конечно, могут быть выбраны равномерно в диапазоне возможных изменений интересующего параметра [19]. Однако такой произвол не всегда уместен. Другим сложным вопросом при расчете границы Баранкина является необходимость решения системы интегральных уравнений, порядок которой соответствует количеству контрольных точек. Существенно, что из соотношения Баранкина также может быть получена как предельный частный случай граница Крамера – Рао. При этом, согласно [21], нижняя граница Баранкина всегда будет больше или равна нижней границе Крамера - Рао (НГКР).
В целом можно заключить, что для решения задачи оценки СКО квадратурных составляющих амплитуд N-OFDM-сигналов по методам, синтезированным в рамках метода максимального правдоподобия в предположении о некоррелированности гауссовых шумов, выбор в пользу границы Крамера - Рао может быть однозначным. Для этого регулярного случая границы Бхаттачария и Баранкина дадут совпадающий с НГКР результат в области больших отношений межсимвольного интервала разбиения амплитуд к величине СКО шумов измерения.
Неравенство Крамера - Рао широко известно и наиболее часто применяется на практике в силу сравнительной простоты его получения. Согласно [19], оно было сформулировано Фишером в 1922 г. и затем было независимо доказано Дюгуа (1937), Эйткином и Сильверстоуном (1942), Фреше (1942), Рао (1945) и Крамером (1946).
При точно известных частотах всех поднесущих сигналов и времени их прихода (режим синхронизированной линии связи) потенциальная точность измерения квадратурных составляющих амплитуд принятых сигналов N-OFDM определяется нижней границей Крамера - Рао:
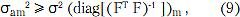
для которой
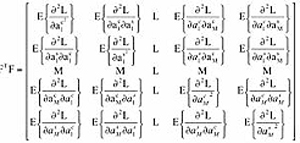
- так называемая информационная матрица Фишера, причем элементы FT F тождественны элементам определителя det в (8) (см. 1-ю часть статьи), σ2 - дисперсия шумов в квадратурной составляющей отклика БПФ-фильтра, Е{...} - символ математического ожидания.
Для некоррелированных отсчетов

где S - размерность БПФ, σ2ADC - дисперсия шума в отсчете АЦП.
Во избежание деления на ноль в соотношениях для характеристик частотных фильтров БПФ удобно при их расчете в (9) воспользоваться известным тождеством:
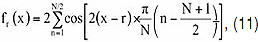
Физический смысл элементов информационной матрицы Фишера в (9), представляющих собой математические ожидания вторых частных производных по оцениваемым параметрам от исходной функции правдоподобия или ее информационного эквивалента, состоит в том, что они характеризуют кривизну пика глобального максимума решающей функции. Чем круче этот пик, тем в меньшем диапазоне значений может бросать оценку параметра при воздействии шумов измерения, тем больше значение второй производной. Другими словами, чем больше значения диагональных элементов информационной матрицы Фишера, тем выше точность оценивания параметров сигналов.
Важно подчеркнуть, что применение нижней границы Крамера - Рао возможно лишь при превышении отношением "сигнал-шум" (в рассматриваемом случае оценивания амплитудных составляющих его роль выполняет отношение межсимвольного интервала разбиения амплитуд в сигнальном созвездии к СКО шумов измерения) некоторого порогового уровня (см. рис. 7 [20]). При этом важно иметь в виду, что участок, обозначенный на рис. 7 как Non-Information, характеризует отсутствие возможности получения состоятельных оценок искомого параметра. В силу сказанного следует учитывать, что для справедливости полученных согласно (9) значений НГКР необходимо обеспечить достаточное превышение интервала разбиения амплитуд над СКО шумов измерения.
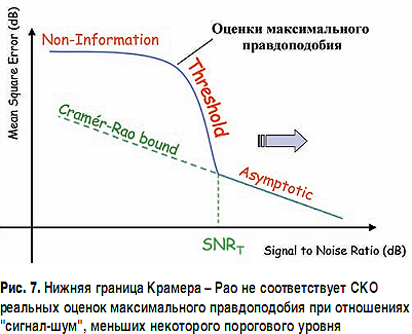
Аналогичный эффект наблюдается и в отношении упоминавшихся границ Бхаттачария и Баранкина (рис. 8 [20]), хотя поведение последней в области сверхмалых значений "сигнал-шум" более адекватно реагирует на потерю работоспособности измерительной процедуры.
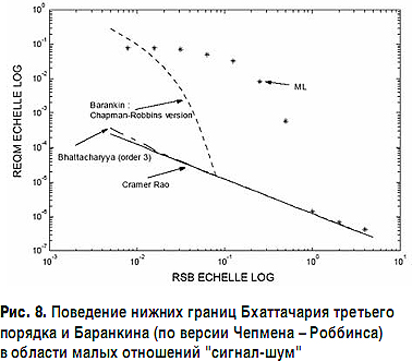
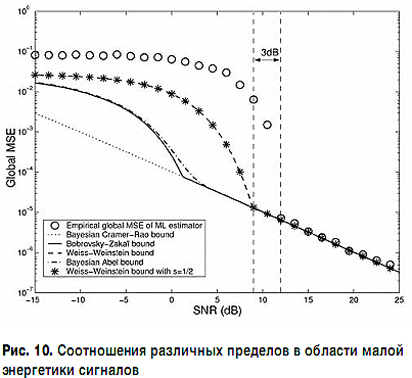
К настоящему времени получен ряд более строгих границ, которые существенно точнее описывают реальный характер изменения значения СКО оценок в области малых отношений "сигнал-шум". Таковыми являются статистические границы Зива – Закаи (Ziv-Zakaп) (рис. 9 [22]), Вайса – Вайнштейна (Weiss-Weinstein), Абеля [23] (рис. 10 [23]) и их модификации [22, 23].
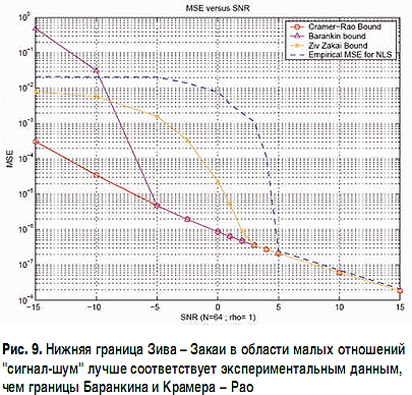
Однако следует отметить, что в области асимптотической эффективности детерминистской границы Крамера – Рао (при больших отношениях "сигнал-шум") указанные статистические пределы СКО от нее практически не отличаются, что лишний раз свидетельствует о правильности сделанного выбора в пользу детального рассмотрения в данной работе лишь НГКР.
Известным ограничением НГКР является также необходимость наличия дифференцируемости решающей функции по неизвестным параметрам. В случае полностью синхронизированного канала связи проблем с операцией дифференцирования функционала правдоподобия в рассматриваемой задаче демодуляции N-OFDM-сигналов не возникает.
Анализ НГКР (9) показывает, что потенциальная точность оценивания квадратурных составляющих амплитуд многочастотного пакета N-OFDM-сигналов определяется прежде всего отношением "сигнал-шум" по выходу синтезированных частотных каналов, а также разносом частот поднесущих в спектральной области. Увеличение пропускной способности, о котором идет речь в случае N-OFDM, может сводиться как к более плотной расстановке поднесущих, так и к сокращению интервала накопления для формирования БПФ-фильтров, сопровождающемуся расширением их полосы пропускания.
Примером доказательства работоспособности рассмотренных здесь процедур обработки N-OFDM-сигналов можно считать экспериментальную апробацию аналогичной совокупности операций над многочастотным пакетом, которая изложена в описании патента РФ на изобретение № 2054684 применительно к измерению АЧХ радиотехнической системы [24].
Аппаратная реализация предложенного подхода сводится к использованию в приемнике информационного сообщения цифрового сигнального процессора или ПЛИС, например, фирмы Xilinx, на базе которых должна осуществляться обработка отсчетов АЦП в соответствии с приведенными в части 1 статьи формульными зависимостями.
Исследование предельных возможностей частотного уплотнения каналов связи на основе N-OFDM-подхода было выполнено путем выборочного расчета дисперсий несмещенных оценок амплитуд как диагональных элементов (9) в случае заданного количества поднесущих. С целью упрощения задачи анализировался сугубо амплитудный метод многоуровневого кодирования, не использующий расквадратуривание сигналов. При этом полагалось, что все поднесущие имеют нулевую начальную фазу и равноотстоят друг от друга по частоте, дисперсия шума, пересчитанная к выходу АЦП, была принята равной единице, шумы квантования не учитывались.
На рис. 11 представлен график зависимости СКО оценки амплитуды (вертикальная ось) от межчастотного интервала (горизонтальная ось), выраженного в долях ширины главного "лепестка" АЧХ-фильтра БПФ по основанию, для двухчастотного N-OFDM-сигнала.
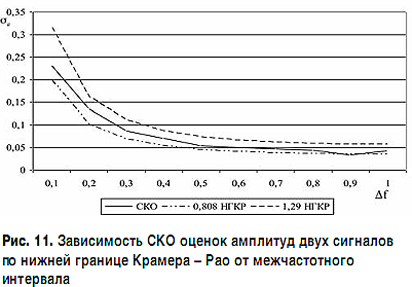
Сплошной линией показано СКО, полученное в результате статистического вычислительного эксперимента, а верхняя и нижняя границы доверительного интервала рассчитаны по теоретической зависимости, полученной из НГКР, для 100 реализаций и доверительной вероятности 0,999.
В случае четырехчастотного пакета величина СКО оценок амплитуд, рассчитанная по НГКР, будет отличаться для сигналов поднесущих, находящихся на краях частотного интервала и внутри него. Чтобы различать указанные поднесущие, вводятся понятия "внешних" и "внутренних" сигналов соответственно (рис. 12).
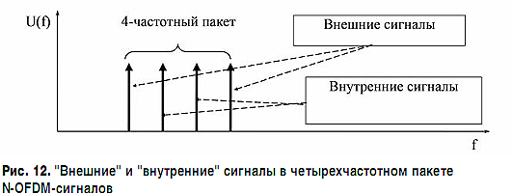
Поднесущие внутри четырехчастотного пакета имеют большее СКО. Это связано с тем, что взаимное влияние поднесущих через боковые лепестки АЧХ-фильтров, синтезированных с помощью БПФ, для внутренних сигналов проявляется более сильно.
Графики СКО оценок амплитуд четырехчастотного N-OFDM-пакета, полученные в результате статистического моделирования, приведены на рис. 13.
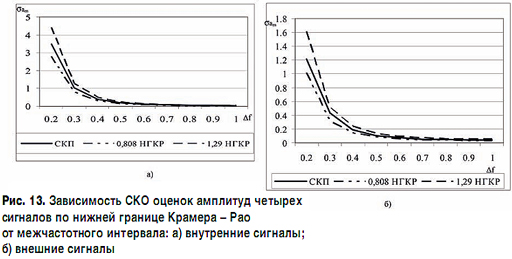
Границы применимости различных видов QAM-модуляции в зависимости от частотного разнесения поднесущих внутренних сигналов приведены на рис. 14, аналогичные пределы в данном случае сохраняются и для внешних сигналов.
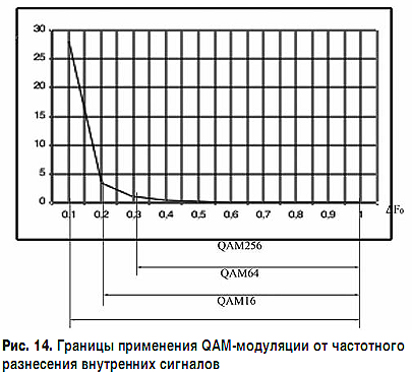
Численные результаты расчета среднеквадратических ошибок измерения амплитуд в квантах АЦП для случая синтеза S частотных фильтров и интервала между поднесущими, представленного в долях ширины фильтра БПФ, обобщены в таблице.
Там же для сравнения даны значения СКО ошибки измерения амплитуды по методу OFDM, полученные расчетным путем. Существенно, что в случае OFDM ошибки измерения амплитуд не зависят от количества используемых поднесущих, тогда как при сверхразрешении эта зависимость проявляется довольно сильно.
Как известно, увеличение разноса частот между каналами требует расширения полосы пропускания аналогового тракта, что зачастую невозможно в радиосистемах, а кроме того, приводит к росту мощности шумов, определяемой по известному выражению:

где ∆f – полоса частот группового канала, N0 – спектральная плотность шума.
Полагая, что ширина АЧХ аналогового тракта строго равна полосе, занимаемой частотными каналами, для корректного сопоставления точностных свойств методов OFDM и N-OFDM необходимо произвести перерасчет полученных для OFDM СКО ошибок измерения амплитуд с учетом необходимости расширения полосы аналогового преселектора при переходе от методов сверхразрешения к процедуре OFDM. Результаты такого пересчета приведены в двух крайних справа столбцах таблицы.
Столбец СКО ошибок измерения амплитуд по методу OFDM в отсутствие пересчета дисперсии шума свидетельствует, что в случае использования процедур сверхразрешения с полосой аналогового тракта, равной полосе сигналов при OFDM-модуляции, сверхразрешение приводит к ухудшению точности оценивания амплитуд сигналов, тем большему, чем больше количество задействованных поднесущих.
При условии строгого согласования полос пропускания аналогового преселектора и частотных каналов двухчастотный метод кодирования со сверхразрешением при разносе поднесущих на полфильтра БПФ позволяет получить более точные оценки амплитуд, чем OFDM. В этом несложно убедиться, cопоставив значения второго слева и второго справа столбцов таблицы. Такое преимущество двухчастотного метода сверхразрешения над OFDM при совпадении полосы преселектора с полосой частотных каналов сохраняется до расстояния между поднесущими почти в четверть ширины фильтра БПФ.
Дальнейшее уплотнение частотных каналов приводит к многократному увеличению СКО ошибок измерения амплитуд (см. четвертый справа столбец таблицы). Однако следует учесть, что при окончательном принятии решения в пользу того или иного метода необходимо учитывать требования, выдвигаемые к точности оценок. По сложившейся практике в классе QAM-кодирования наиболее распространенной в качестве предельной по плотности упаковки бит в одном боде является модуляция 256QAM, предполагающая разбиение амплитуды сигнала на 8 уровней вдоль каждой из квадратурных составляющих. При использовании, например, 13-разрядного АЦП общее количество квантов сигнальной смеси, как известно, составляет 8192 или, с учетом знакового разряда, 4096 в каждой полярности. Если разделить это число на количество уровней в сигнальном созвездии, то получим, что на каждый уровень амплитуды отводится 512 квантов АЦП. Для надежного декодирования информации можно положить, что интервал между точками в сигнальном созвездии (уровнями амплитуд) должен составлять 6σа, где σа – СКО ошибки измерения амплитуды сигнала, не зависящее от номинала амплитудного уровня. С учетом этого допустимая величина σа может быть определена из равенства 6σа = 512 и составляет 512/6 ≈ 85 квантов. При таких ограничениях на точность измерения, согласно данным таблицы, для "квартета" поднесущих, уже начиная с 16-точечной протяженности измерительной выборки, реализация сверхрелеевского разрешения позволяет обеспечить надежную связь при расстановке частот сигналов с шагом в 1/8 ширины синтезированного БПФ-фильтра. Общая полоса частотного пакета при этом ограничена половиной ширины фильтра БПФ, что соответствует 8-кратному частотному уплотнению по сравнению с традиционным OFDM. Таким образом, в рассмотренном примере неоправданно высокая точность измерения амплитуд по OFDM, достигаемая ценой расширения полосы частотного пакета, оказалась намного превосходящей требуемую. Прецизионность измерений в OFDM неадекватна и точности формирования информационных сообщений на передающей стороне, где квант цифроаналогового преобразователя, подобно АЦП приемника, как правило, соответствует среднеквадратическому значению шума. Поэтому представляется возможным в рамках QAM-модуляции и ей подобных, несмотря на ухудшение точности амплитудных измерений, пойти на использование сверхразрешения сигналов по методу N-OFDM, достигая большей компактности каналов связи в спектральной области.
В целом увеличение степени частотного уплотнения либо же ее сохранение на заданном уровне при росте количества поднесущих может достигаться повышением разрядности АЦП до 14, 16 и более разрядов, а также увеличением длительности измерительной выборки в периодах дискретизации. Например, за время миллисекундного интервала существования полезного сигнала в стандарте цифрового телевидения DVB-T при использовании АЦП с частотой преобразования 100 МГц может быть сформировано 100 тыс. отсчетов АЦП. Впрочем, для столь значительных протяженностей сигнальных выборок серьезным ограничением является необходимость реализации всех вычислений в реальном масштабе времени. Для решения этой проблемы следует использовать децимацию (прореживание) отсчетов АЦП, например путем их дополнительного стробирования [25, 26], однако такой подход заслуживает отдельного рассмотрения.
В результате исследования допустимых пределов частотного уплотнения было установлено, что максимальное количество N-OFDM поднесущих в одном фильтре нецелесообразно задавать больше пяти, поскольку в противном случае для реализации приемлемой точности измерения амплитудных составляющих требуется весьма значительное отношение "сигнал-шум" либо довольно длительная выборка отсчетов (64 и более). При использовании 8 поднесущих реально можно говорить о достижении четырехкратного уплотнения информационного потока.
При большем количестве гармонических поднесущих их расстановку в частотной области целесообразно осуществлять в виде четырехсигнальных блоков с разносом между такими "квартетами" по частоте, например, в 2 раза превышающим интервал между поднесущими сигналов внутри указанного блока (рис. 15). При этом для пакета из 16 поднесущих максимальный выигрыш в пропускной способности фактически ограничивается трехкратной величиной.
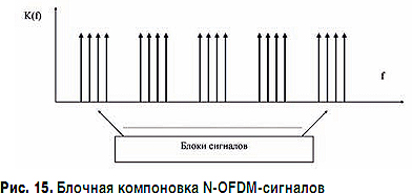
В общем случае полосу частот, занимаемую M поднесущими, равномерно скомпонованными в нескольких идентичных блоках, можно рассчитать по формуле
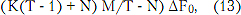
где T – количество поднесущих в отдельно взятом блоке, K – интервал между поднесущими внутри блока из T сигналов, N – межблочный интервал, ΔF0 – ширина фильтра БПФ.
Для указанной структуры пакета из M = 16 поднесущих при T = 4 и K = 0,5, N = 2 диапазон частот, занимаемых N-OFDM-сигналами, составляет 12ΔF0. Полагая, что аналогичный OFDM-пакет имеет ширину спектра 15ΔF0 и точность оценивания амплитуд N-OFDM-сигналов соответствует заданной, получим выигрыш в ширине спектральной полосы (1 - 12/15)∙100% = 20%. К примеру, для частотного канала с полосой 40 МГц переход к N-OFDM-сигналам с учетом указанных условий позволяет сэкономить 8 МГц частотного ресурса.
Опираясь на рассмотренную методику, можно проанализировать предельные возможности спектрального уплотнения и для более представительных частотных множеств. В частности, на рис. 16 представлены результаты расчета НГКР для N-OFDM-пакета из 32 поднесущих при двух вариантах их блочной компоновки.
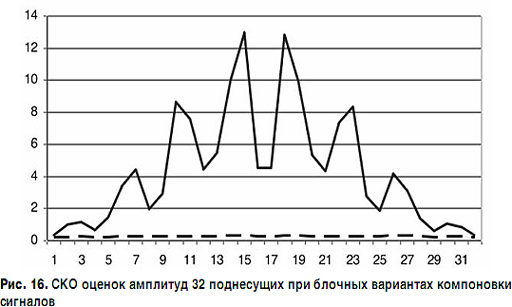
Сплошная линия соответствует зависимости СКО в квантах АЦП от номера поднесущей в случае равномерного расположения частот внутри блока в соответствии со схемой (рис. 15), при этом интервал между поднесущими внутри каждого блока одинаков и равен 0,5 ширины фильтра БПФ ΔF0, а между блоками – 2ΔF0. Согласно приведенной выше формуле полоса частот такого N-OFDM-пакета составляет (3∙0,5∙ΔF0+2∙ΔF0)∙8 – 2∙ΔF0 = 26ΔF0 вместо 31ΔF0 в случае OFDM. В процентном выражении дополнительное частотное уплотнение, достигаемое при N-OFDM в сравнении с OFDM, составляет (1 - 26/31)∙100% ≈ 16,13%.
Штриховой линией на графике (рис. 16) показаны значения СКО амплитуд поднесущих, размещение которых соответствует схеме иерархической блочной компоновки с интервалами 0,25 ΔF0 – 1 ΔF0 – 0,25 ΔF0 – 2 ΔF0 (рис. 17).
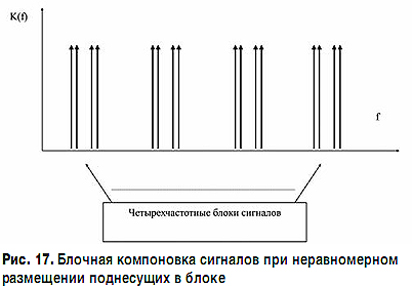
При такой структуре блоков общая полоса частот N-OFDM-сигнала остается неизменной и по-прежнему равна 26ΔF0, что позволяет высвободить те же 16,13% частотного ресурса по сравнению с OFDM-пакетом. Однако величина СКО при этом стала почти одинаковой для всех поднесущих и, главное, не превышает 0,5 кванта АЦП. Данный результат свидетельствует об эффективности блочного расположения поднесущих в N-OFDM-сигналах и открывает широкие возможности по его оптимизации, например на основе фрактальных схем типа канторовых множеств и т.д.
Неэквидистантное расположение сигналов внутри блоков целесообразно дополнить адаптивным изменением интервалов между поднесущими в блоках и межблочных дистанций в зависимости от конкретной помеховой обстановки в канале или допплеровского смещения частоты. На этой же основе возможна маскировка передаваемой информации за счет манипуляции частотными интервалами по заранее установленной схеме.
Потенциально удвоить скорость передачи информации, как известно, позволяет переход к использованию сигналов двойной поляризации. В случае сигналов N-OFDM применение ортогональной поляризации излучения было предложено в [27]. Однако приведенные в [27] результаты исследований не касались особенностей обработки сигналов N-OFDM в цифровых антенных решетках (ЦАР). В то же время применение ЦАР в сочетании с принципом MIMO позволяет существенно повысить не только скорость передачи, но и помехозащищенность средств связи. Поэтому рассмотренные здесь основы теории цифровой обработки N-OFDM-сигналов в дальнейшем были обобщены автором применительно к MIMO-системам и продолжают совершенствоваться в рамках соответствующей научной школы (см. сайт www.slyusar.kiev.ua), в том числе в многопользовательском варианте реализации MIMO-технологий.
Литература
Опубликовано: Журнал "Технологии и средства связи" #6, 2013
Посещений: 6373
Статьи по теме
Автор
| |||
В рубрику "Решения операторского класса" | К списку рубрик | К списку авторов | К списку публикаций